DU A Unit Admission Question Solution 2020-2021

DU A Unit Admission Question Solution 2020-2021

নিচের ভিডিওতে দেখে নাও বিস্তারিত:

কোর্সটি কিনতে পাশের বাটনটি ক্লিক কর:   

 

কোর্সের ডেমো ভিডিও(এভাবে পদার্থবিজ্ঞান+রসায়ন+উচ্চতরগণিত এর বিগত বিশ বছরের সকল প্রশ্নের সমাধান থাকবে ভিডিওতে)

 

পদার্থবিজ্ঞান

1. একটি সমান্তরাল পাত ধারককে চার্জিত করার পর ব্যাটারি খুলে ফেলা হলো। এ অবস্থায় ধারকটিতে সঞ্চিত শক্তির পরিমাণ \(U_{0}\)। পাত দুটির দূরত্ব যদি দ্বিগুণ করা হয়, তবে ধারকে সঞ্চিত শক্তি কতগুন হবে?
   1. \(\frac{U_{0}}{2}\)
   2. \(\frac{U_{0}}{4}\)
   3. \(2 U_{0}\)
   4. \(4 U_{0}\)

   Ans. \(2 U_{0}\)

2. q আধান বিশিষ্ট একটি গােলককে একটি অপরিবাহী সূতার একপ্রান্ত বেঁধে \(\omega\) কৌণিক বেগে ঘােরানো
   হচ্ছে। ঘূর্ণায়মান আধানটি কী পরিমাণ বিদ্যুৎ উৎপন্ন করবে?
   1. \(\omega q\)
   2. \(2 \pi \omega q\)
   3. \(\frac{q}{\omega}\)
   4. \(\frac{q \omega}{2 \pi}\)

   Ans. \(\frac{q \omega}{2 \pi}\)

3. স্থিতিস্থাপক গুণাংকের মাত্রা কী?
   1. \(\mathrm{MLT}^{-1}\)
   2. \(\mathrm{ML}^{-1} \mathrm{~T}^{-2}\)
   3. \(\mathrm{MLT}^{-2}\)
   4. \(\mathrm{ML}^{2} \mathrm{~T}^{-2}\)

   Ans. \(\mathrm{ML}^{-1} \mathrm{~T}^{-2}\)

4. কোন ত্রুটি দূরীকরণে উত্তল লেন্স ব্যবহার করা হয়?
   1. ক্ষীণ দৃষ্টি
   2. দূর দৃষ্টি
   3. চালশে
   4. বিষম দৃষ্টি

   Ans. দূর দৃষ্টি

5. \({ }_{13}^{27} \mathrm{Al}+{ }_{2}^{4} \mathrm{He} \rightarrow{ }_{14}^{30} \mathrm{Si}+()\) নিউক্লীয় বিক্রিয়াতে অনুপস্থিত কণাটি হল-
   1. আলফা কণা
   2. প্রোটন
   3. ইলেকট্রন
   4. নিউট্রন

   Ans. প্রোটন

6. একটি সরল দোলকের দোলনকাল 50% বাড়াতে এর কার্যকর দৈর্ঘ্যের পরিবর্তন কত হবে?
   1. 25%
   2. 100%
   3. 125%
   4. 67%

   Ans. 125%

7. কোনো আদর্শ গ্যাসের তাপমাত্রা কেলভিন স্কেলে 4 গুণ বৃদ্ধি পেলে তার অণুগুলোর মূল গড় বর্গবেগ কত গুণ বৃদ্ধি পায়?
   1. 4
   2. \(1 / 2\)
   3. 2
   4. 1

   Ans. 2

8. 14 মিনিট পরে একটি তেজস্ক্রিয় মৌলের \(\frac{1}{16}\) অংশ অবশিষ্ট থাকে। এর অর্ধায়ু হবে-
   1. \(\frac{7}{8} \mathrm{~min}\)
   2. \(\frac{7}{4} \mathrm{~min}\)
   3. \(\frac{7}{2} \mathrm{~min}\)
   4. \(\frac{14}{3} \mathrm{~min}\)

   Ans. \(\frac{7}{2} \mathrm{~min}\)

9. কোনো দিক পরিবর্তী তড়িচ্চালক বলের গড়বর্গের বর্গমূল মান 10 volt। তড়িচ্চালক বলের শীর্ষমান হলো-
   1. 10.00 volt
   2. 5.00 volt
   3. 1.41 volt
   4. 14.14 volt

   Ans. 14.14 volt

10. a এর মান কত হলে \(\vec{A}=2 \hat{\imath}+2 \hat{\jmath}-\hat{k}\) এবং \(\overrightarrow{\mathrm{B}}=a \hat{\imath}+\hat{\jmath}\) ভেক্টরদ্বয় পরস্পর লম্ব হবে?
    1. 0
    2. \(\frac{7}{4} \)
    3. \(-1\)
    4. 2

    Ans. \(-1\)

11. কত বেগে চললে একটি রকেটের গতিশীল দৈর্ঘ্য এর নিশ্চল দৈর্ঘ্যের অর্ধেক হবে?
    1. \(\frac{1}{2} c\)
    2. \(\frac{\sqrt{3}}{2} c\)
    3. \(\frac{3}{\sqrt{2}} C\)
    4. \(\frac{3}{4} C\)

    Ans. \(\frac{\sqrt{3}}{2} c\)

12. একটি m ভরের বস্তু ঘর্ষণবিহীন একটি তলে v বেগে চলার সময় একটি স্প্রিং-এর সাথে ধাক্কা লেগে স্প্রিংটিকে সংকুচিত করল। স্প্রিংটির বল-ধ্রুবক k হলে স্প্রিংটি কতটুকু সংকুচিত হবে?
    1. \(\sqrt{\frac{m}{k}} v\)
    2. \(\sqrt{\frac{k}{m}} v\)
    3. \(\sqrt{k v}\)
    4. \(\sqrt{m v}\)

    Ans. \(\sqrt{\frac{m}{k}} v\)

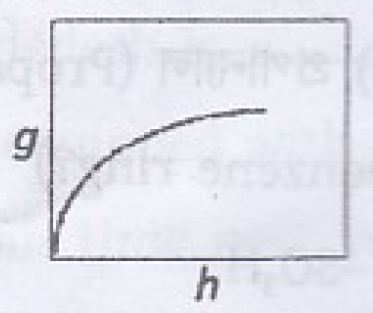
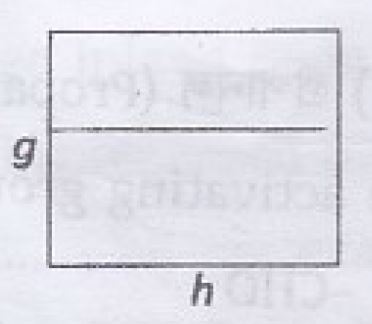
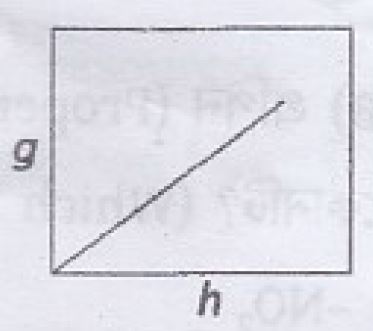
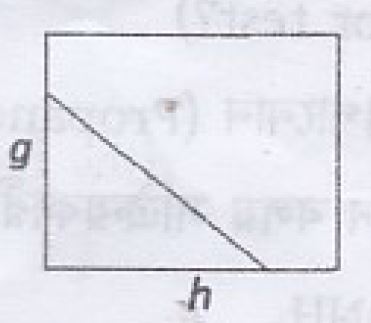
13. অভিকর্ষীয় ত্বরণ g বনাম পৃথিবী পৃষ্ঠ হতে গভীরতা h এর লেখচিত্র কোনটি?
    1. 
    2. 
    3. 
    4. 

    Ans.

14. ইয়ং এর দ্বি-চির পরীক্ষণের চিরদ্বয়ের মধ্যবর্তী দূরত্ব হলো d এবং চিরদ্বয় থেকে পর্দা D দূরত্বে অবস্থিত।
    পর্দার উপর প্রতি একক প্রস্থে ডোরার সংখ্যা হলো-
    1. \(\frac{D}{d \lambda}\)
    2. \(\frac{d}{D \lambda}\)
    3. \(\frac{\lambda}{D d}\)
    4. \(\frac{d^{2}}{\lambda D^{3}}\)

    Ans. \(\frac{d}{D \lambda}\)

15. একটি বস্তু 12 m ব্যাসার্ধের একটি বৃত্তাকার পথে চলমান আছে। একটি মুহূর্তে বৃত্তাকার পথে এর দ্রুতি
    6 m/s এবং এটি \(4 \mathrm{~m} / \mathrm{s}^{2}\) হারে বৃদ্ধি পাচ্ছে। ঐ মুহূর্তে বস্তুটির ত্বরণের মান কত?
    1. \(2 \mathrm{~m} / \mathrm{s}^{2}\)
    2. \(3 \mathrm{~m} / \mathrm{s}^{2}\)
    3. \(4 \mathrm{~m} / \mathrm{s}^{2}\)
    4. \(5 \mathrm{~m} / \mathrm{s}^{2}\)

    Ans. \(5 \mathrm{~m} / \mathrm{s}^{2}\)

পদার্থবিজ্ঞান লিখিত অংশ

১।একজন বাইসাইকেল আরোহী সমতল বক্র পথে v বেগে ভ্রমণ করছে। সাইকেলের চাকা এবং পথের মধ্যকার স্থিতি ঘর্ষন গুনাংক \(\mu_{s}=0.50\)। সাইকেলের উপর ক্রিয়ারত বল সমূহের নাম লিখ। যদি বেগ v = 10 m/s হয়, তবে সর্বনিম্ন কত ব্যাসার্ধের বৃত্তাকার পথে আরোহীটি ভ্রমণ করতে পারবে?

---

ক্রিয়ারত বলসমূহ:

1. ওজন
2. ঘর্ষণ বল
3. তলের উল্লম্ব প্রতিক্রিয়া

কেন্দ্রমুখী বল = ঘর্ষণ বল
বা, \(\frac{m v^{2}}{r}=\mu R\)
বা, \(\frac{m v^{2}}{r}=\mu m g\)
বা, \(\frac{v^{2}}{r}=\mu g\)
বা, \(r=\frac{v^{2}}{\mu g}\)
বা, \(r=\frac{10^{2}}{0.5 \times 10}\)
\(\therefore r=20 m\) (Ans.)

২। একটি উত্তল লেন্সের ফোকাস দূরত্ব 10 cm। লেন্সের বাম পাশে 30 cm দূরে একটি বস্তু রাখা হলো।
প্রতিবিম্বের অবস্থান, প্রকৃতি ও বিবর্ধন নির্ণয় কর।

---

  \(f=10 \mathrm{~cm}\)
  \(u=30 \mathrm{~cm}\)
 \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
বা, \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
বা, \(\frac{1}{v}=\frac{1}{10}-\frac{1}{30}\)
বা, \(\frac{1}{v}=\frac{3-1}{30}\)
বা, \(\frac{1}{v}=\frac{2}{30}\)
বা, \(\frac{1}{v}=\frac{1}{15}\)
বা, \(v=15\)
বা, বিবর্ধন, \(m=-\frac{v}{u}\)
   \(=-\frac{15}{30}\)
   \(=-0.5\)
বাস্তব, উল্টো, খর্বিত বিম্ব গঠিত হবে।

---

৩। চিত্রের বর্তনীটির \(4.0 \Omega\) রোধের প্রান্তদ্বয়ের মধ্যে বিভব পার্থক্য কত হবে?

---

\(R=\frac{2}{3}+\left(\frac{1}{2}+\frac{1}{4}\right)^{-1}\)
\(R=\frac{2}{3}+\left(\frac{2+1}{4}\right)^{-1}\)
 \(=\frac{2}{3}+\frac{4}{3}\)
 \(=\frac{2+4}{3}\)
 \(=2 \Omega\)
\(I=\frac{V}{R}=\frac{2}{2}=1 A\)
\(\frac{2}{3} \Omega\) রোধের বিভব, \(V_{\frac{2}{3}}=\frac{2}{3} \times 1=\frac{2}{3} V\)
\(4.0 \Omega\) রোধের বিভব \(=2-\frac{2}{3}\)
 \(=\frac{6-2}{3}\)
 \(=\frac{4}{3} V\)

---

৪। একটি কার্নো ইঞ্জিন \(T_{H}=900 \mathrm{~K}\) এবং \(T_{L}=300 \mathrm{~K}\) তাপমাত্রার মধ্যে কার্যরত। ইঞ্জিনটি প্রতি চক্রে 0.25 s
সময়ে 1200 J কাজ করে। উচ্চ তাপমাত্রায় ধারক থেকে শক্তি স্থানান্তরের ফলে এর কার্যকরী পদার্থের (অর্থাৎ আদর্শ গ্যাসের) এনট্রপি বৃদ্ধি বের কর।

---

  \(\frac{T_{H}}{T_{L}}=\frac{Q_{H}}{Q_{L}}\)
বা, \(\frac{900}{300}=\frac{Q_{H}}{Q_{L}}\)
বা, \(Q_{H}=3 Q_{L}\)
 \(W=Q_{H}-Q_{L}\)
বা, \(1200=3 Q_{L}-Q_{L}\)
বা, \(1200=2 Q_{L}\)
\(Q_{L}=600 \mathrm{~J}\)
\(\therefore Q_{H}=3 \times 600=1800 \mathrm{~J}\)
\(\Delta S_{H}=\frac{Q_{H}}{T_{H}}\)
  \(=\frac{1800}{900} \mathrm{JK}^{-1}\)
  \(=2 \mathrm{JK}^{-1}\)
  \(=2 \times 4 w k^{-1}\)
  \(=8 w k^{-1}\)

---

রসায়ন

1. বিশুদ্ধ পানিতে \(\mathrm{OH}^{-}\) এবং \(\mathrm{H}^{+}\) এর মোলার ঘনমাত্রা এর অনুপাত কত?
   1. 7

   2. \(10^{-7}\)
   3. 0

   4. 1

   Ans. 1

2. অষ্টক সম্প্রসারণ এর উদাহরণ কোনটি?

   1. \(\mathrm{BeCl}_{2}\)
   2. \(\mathrm{PCl}_{5}\)
   3. \(\mathrm{BCl}_{3}\)
   4. \(\mathrm{Cl}_{2}\)

   Ans. \(\mathrm{PCl}_{5}\)

3. নিচের কোন তড়িৎদ্বারটির প্রমাণ বিজারণ বিভবের মান সবচেয়ে কম?
   1. \(\mathrm{H}^{+}(\mathrm{aq}) / \mathrm{H}_{2}(\mathrm{~g}), \mathrm{Pt}\)
   2. \(\mathrm{Cu}^{2+}(\mathrm{aq}) / \mathrm{Cu}(\mathrm{s})\)
   3. \(\mathrm{Na}^{+}(\mathrm{aq}) / \mathrm{Na}(\mathrm{s})\)
   4. \(\mathrm{Pt}(\mathrm{s}) / \mathrm{F}(\mathrm{g}) / \mathrm{F}^{-}(\mathrm{aq})\)

   Ans. \(\mathrm{Na}^{+}(\mathrm{aq}) / \mathrm{Na}(\mathrm{s})\)

4. aA → bB বিক্রিয়াটির ক্ষেত্রে কোনটি বিক্রিয়ার হার নির্দেশ করে?
   1. \(-\frac{\mathrm{d}[\mathrm{A}]}{\mathrm{d} t}\)
   2. \(-\frac{1}{a} \frac{d[A]}{d t}\)
   3. \(-\frac{d[B]}{d t}\)
   4. \(-\frac{1}{b} \frac{d[A]}{d t}\)

   Ans. \(-\frac{1}{a} \frac{d[A]}{d t}\)

5. দুধের প্রোটিন কোনটি?
   1. ক্যারোটিন
   2. লিপিড
   3. ক্যাসিন
   4. ল্যাক্টাঅ্যালবুমিন

   Ans. ক্যাসিন

6. নিচের কোন যৌগটি সিলভার দর্পণ পরীক্ষা দেয়?
   1. প্রপানোন
   2. প্রপিন
   3. প্রপানল
   4. প্রপান্যাল

   Ans. প্রপান্যাল

7. বেনজিন বলয় সক্রিয়কারী মূলক কোনটি?
   1. \(-\mathrm{NH}_{2}\)
   2. \(-\mathrm{NO}_{2}\)
   3. -CHO
   4. \(-\mathrm{SO}_{3} \mathrm{H}\)

   Ans. \(-\mathrm{NH}_{2}\)

8. NaCl-এর সাথে \(\mathrm{H}_{2} \mathrm{O}\) যোগ করলে কোনটি ঘটে?
   1. \(\mathrm{Na}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)
   2. \(\mathrm{NaOH}(\mathrm{aq})+\mathrm{HCl}(\mathrm{aq})\)
   3. \(\mathrm{OH}^{-}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)
   4. \(\mathrm{Na}^{+}+\mathrm{Cl}^{-}\)

   Ans. \(\mathrm{Na}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

9. হাইড্রোনিয়াম আয়নে কোন কোন বন্ধন বিদ্যমান?
   1. আয়নিক ও সমযোজী বন্ধন
   2. আয়নিক ও সন্নিবেশ বন্ধন
   3. সমযোজী ও সন্নিবেশ বন্ধন
   4. আয়নিক ও হাইড্রোজেন বন্ধন

   Ans. সমযোজী ও সন্নিবেশ বন্ধন

10. নিচের কোনটি সত্য নয়?
    1. \(\mathrm{K}_{w}=1 \times 10^{-14}\)
    2. \(\mathrm{pK}_{w}=14\)
    3. \(\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=\mathrm{K}_{w}\)
    4. \(K_{w}=1 \times 10^{14} M\)

    Ans. \(K_{w}=1 \times 10^{14} M\)

11. ক্রোমিক এসিড দ্বারা কাঁচপাত্র পরিষ্কার করার সময় কোন ধরনের বিক্রিয়া ঘটে?
    1. জারণ
    2. প্রতিস্থাপন
    3. প্রশমন
    4. বিজারণ

    Ans. জারণ

12. As- এ কয়টি যোজন ইলেকট্রন আছে?
    1. 3
    2. 4
    3. 5
    4. 6

    Ans. 5

13. অ্যালকাইল হ্যালাইডের E2 অপসারণ বিক্রিয়ায়, অ্যালকোহলিক KOH/NaOH এর ভূমিকা হলো-
    1. ক্ষার
    2. দ্রাবক
    3. অনুঘটক
    4. নিউক্লিওফাইল

    Ans. ক্ষার

14. \(\mathrm{R}_{\mathrm{H}}\) রিডবার্গ ধ্রুবক হলে, হাইড্রোজেন পরমাণুর বর্ণালিতে বামার সিরিজের জন্য সর্বনিম্ন কত তরঙ্গ, সংখ্যার রশ্মি বিকিরিত হয়?
    1. \(\frac{3}{4} \mathrm{R}_{\mathrm{H}}\)
    2. \(\frac{5}{36} \mathrm{R}_{\mathrm{H}}\)
    3. \(\frac{3}{16} \mathrm{R}_{\mathrm{H}}\)
    4. \(\frac{9}{144} \mathrm{R}_{\mathrm{H}}\)

    Ans. \(\frac{5}{36} \mathrm{R}_{\mathrm{H}}\)

15. নিম্নের বিক্রিয়াগুলো হতে কার্বনের গণনাকৃত দহন তাপ হলো-
    (i) \(\mathrm{C}(\mathrm{s})+1 / 2 \mathrm{O}_{2}(\mathrm{~g}) \rightarrow \mathrm{CO}(\mathrm{g}) \quad \Delta \mathrm{H}=-111 \mathrm{~kJ} / \mathrm{mol}\)
    (ii) \(\mathrm{CO}(\mathrm{g})+1 / 2 \mathrm{O}_{2}(\mathrm{~g}) \rightarrow \mathrm{CO}_{2}(\mathrm{~g}) \Delta \mathrm{H}=-283 \mathrm{~kJ} / \mathrm{mol}\)
    1. 173 \(\mathrm{~kJ} / \mathrm{mol}\)
    2. -394 \(\mathrm{~kJ} / \mathrm{mol}\)
    3. 373 \(\mathrm{~kJ} / \mathrm{mol}\)
    4. 394 \(\mathrm{~kJ} / \mathrm{mol}\)

    Ans. -394 \(\mathrm{~kJ} / \mathrm{mol}\)

রসায়ন (chemistry) লিখিত অংশ

৫। (ক) রাসায়নিক বন্ধন কী? ন্যাফথালিন অণুতে কয়টি এবং কী কী বন্ধন বিদ্যমান?
রাসায়নিক বন্ধন: একটি রাসায়নিক বন্ধন পরমাণু, আয়ন বা অণুর মধ্যে একটি স্থায়ী আকর্ষণ যা রাসায়নিক যৌগ গঠন করে।
ন্যাফথালিন অণুতে মোট 24টি বন্ধন রয়েছে যার মধ্যে 5টি পাই বন্ধন এবং 19টি সিগমা বন্ধন।

---

(খ) প্রাইমারি, সেকেন্ডারি ও টারসিয়ারি অ্যালকোহলকে কীভাবে আলাদা করা যায়?

---

গাঢ় HCl এ \(ZnCl_2\) এর দ্রবণকে ‍লুকাস বিকারক বলে যা \(3^o\) অ্যালকোহলের সাথে বিক্রিয়ার করে সাথে সাথেই অ্যালকাইল ক্লোরাইডের সাদা অধ:ক্ষেপ তৈরি করে, \(2^o\) অ্যালকোহলের সাথে আস্তে আস্তে বিক্রিয়ার করে(5-10 মিনিটে) অ্যালকাইল ক্লোরাইডের অধ:ক্ষেপ তৈরি করে এবং \(1^o\) অ্যালকোহলের সাথে কক্ষ তাপমাত্রায় কোন বিক্রিয়ার করে না তবে মিশ্রণকে উত্তপ্ত করলে অতী ধীরে অ্যালকাইল ক্লোরাইড তৈরি করে।

---

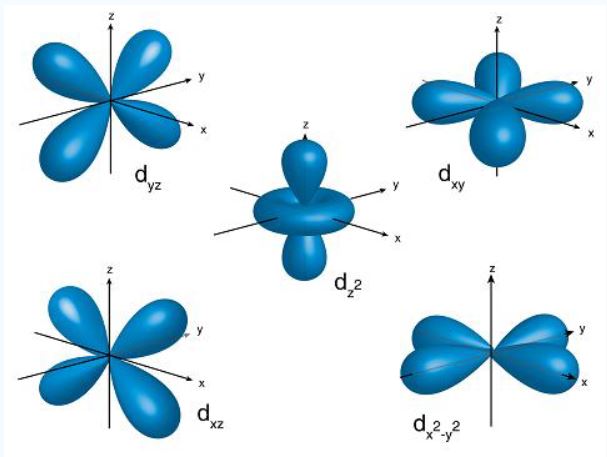
৬। অরবিটাল কী? পাঁচটি d-অরবিটালের নাম লিখ এবং এদের দ্বি-মাত্রিক চিত্র অংকন কর। তড়িৎ ঋণাত্মকতা এবং ইলেক্ট্রন আসক্তির মধ্যে প্রধান পার্থক্য কী?

---

অরবিটাল:নিউক্লিয়াসের চতুর্দিকে ইলেকট্রনের আবর্তনের সর্বাধিক সম্ভাব্য অঞ্চলকে অরবিটাল বলে।

গ্যাসীয় অবস্থায় কোনো মৌলের এক মোল গ্যাসীয় পরমাণুতে এক মোল ইলেকট্রন প্রবেশ করিয়ে এক মোল ঋণাত্মক আয়নে পরিণত করতে যে শক্তি দরকার, তাকে ঐ মৌলের ইলেকট্রন আসক্তি বলে। আর দুটি পরমাণু যখন সমযোজী বন্ধনে আবদ্ধ হয় তখন অণুর পরমাণুগুলো বন্ধনের ইলেকট্রন দুটিকে নিজের দিকে আকর্ষণ করে। এই আকর্ষণকে তড়িৎ ঋণাত্মকতা বলে।

---

৭।(ক)
(i) \(\mathrm{X} \stackrel{\mathrm{K} \mathrm{O} \mathrm{H}(\mathrm{aq})}{\longrightarrow} \mathrm{Y} \stackrel{[0]}{\rightarrow} \mathrm{Z}\)
(ii) \(\mathrm{Z}+2,4-\mathrm{DNPH} \rightarrow\) Yellow precipitate
(iii) \(\mathrm{Z}+\) Fehling solution \(\rightarrow\) No change
(iv) \(X\) is the isomer of \(C_{4} H_{9} B r\)

উপরের তথ্যগুলো ব্যবহার করে উপযুক্ত যুক্তিসহ X, Y এবং Z এর গাঠনিক সংকেত নির্ণয় কর।

---

(ii) নং শর্তমতে z একটি কার্বনিল যৌগ এবং (iii) নং শর্ত হতে বুঝা যায় তা কিটোন। (iv) নং শর্তমতে \(X\) হলো \(C_{4} H_{9} B r\) এর সমাণু পরবর্তীতে যা হতে অ্যালকোহল Y এবং কিটোন Z উৎপন্ন হয় তাই X এ Br অবশ্যই 2 নয় কার্বনে আছে।
X হলো: \(\mathrm{CH}_{3}-\mathrm{CH}_{2}-\mathrm{CHBr}-\mathrm{CH}_{3}\)

Y হলো:\(\mathrm{CH}_{3}-\mathrm{CH}_{2}-\mathrm{CH}(\mathrm{OH})-\mathrm{CH}_{3}\)

Z হলো:\(\mathrm{CH}_{3}-\mathrm{CH}_{2}-\mathrm{CO}-\mathrm{CH}_{3}\)

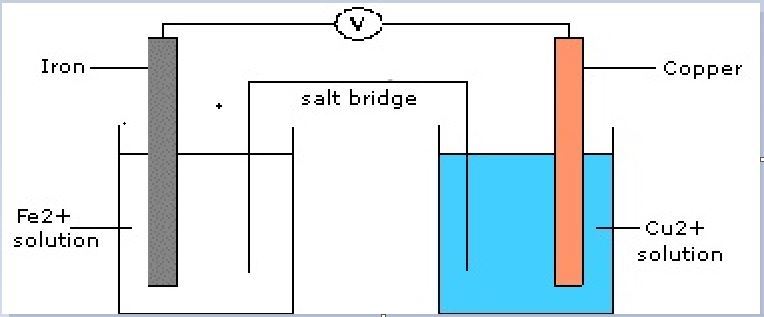
(খ) লবন সেতু ও তড়িৎদ্বার \(\left[(\mathrm{i}) \mathrm{Fe}^{2+}(\mathrm{aq}) / \mathrm{Fe}(\mathrm{s})=-0.44 \mathrm{~V} \text { এবং (ii) } \mathrm{Cu}^{2+}(\mathrm{aq}) / \mathrm{Cu}(\mathrm{s})=0.34 \mathrm{~V}\right]\) ব্যবহার করে, তড়িৎ কোষটির চিত্র অঙ্কন কর এবং কোষের emf নির্ণয় কর।

---

কোষ বিক্রিয়া: \(F e / F e^{2+} \| C u^{2+} / C u\)
\(E_{\text {cell }}^{o}=E_{F e}^{o} / F e^{2+}+E_{C u^{2+}}^{o} / C u\)
  \(=0.44+0.34\)
  \(=0.78 \mathrm{~V}\)

৮। ইথানয়িক এসিডের জলীয় দ্রবণের বিয়োজন সাম্যবস্থা দেখাও এবং এর \(\mathrm{K}_{\mathrm{a}}\) সংজ্ঞায়িত কর। কোন শর্তে,
\(\mathrm{pK}_{\mathrm{a}}=\mathrm{pH}\) হবে, প্রয়োজনীয় সমীকরণসহ ব্যাখ্যা কর।

---

\(\mathrm{CH}_{3} \mathrm{COOH} \rightleftharpoons \mathrm{CH}_{3} \mathrm{COO}^{-}+\mathrm{H}^{+}\)
\(K_{a}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}\)
\(p H=p k_{a}+\log \frac{[\text { Salt }]}{[\text { Acid }]}\)
\(p H=p k_{a}\) হবে যদি,
\(\log \frac{[\text { Salt }]}{[\text { Acid }]}=0\)
বা, \(\log \frac{[\text { Salt }]}{[\text { Acid }]}=\log 1\)
বা, \(\frac{[\text { Salt }]}{[\text { Acid }]}=1\)
বা, \([\) Salt \(]=[\) Acid \(]\)

উচ্চতর গণিত

1. \(2 x=y^{2}+8 y+22\) পরাবৃত্তের শীর্ষবিন্দুর স্থানাংক হবে-
   1. (3,-4)
   2. (-3, 4)
   3. (-3, -4)
   4. (3, 4)

   Ans. (3,-4)

2. \(\lim _{x \rightarrow 0} \frac{1-\cos x}{\sin ^{2} 2 x}\) এর মান হবে-
   1. \(\frac{1}{4}\)
   2. \(\frac{1}{8}\)
   3. \(\frac{1}{2}\)
   4. 1

   Ans. \(\frac{1}{8}\)

3. \(\int_{0}^{2}|x-1| d x=?\)
   1. 0
   2. 1
   3. 2
   4. \(\frac{1}{2}\)

   Ans. 1

4. তিনটি ছক্কা একবার নিক্ষেপ করা হলে তিনটিতেই একই সংখ্যা পাওয়ার সম্ভাবনা কত?
   1. \(\frac{1}{18}\)
   2. \(\frac{1}{6}\)
   3. \(\frac{1}{216}\)
   4. \(\frac{1}{36}\)

   Ans. \(\frac{1}{36}\)

5. \(\frac{d}{d x}\left(\cos ^{2}(\ln x)\right)=?\)
   1. \(-\frac{\sin (2 \ln x)}{2}\)
   2. \(-\frac{2 \cos (\ln x)}{x}\)
   3. \(-\frac{\sin (2 \ln x)}{x}\)
   4. \(-2 x \cos (\ln x) \sin (\ln x)\)

   Ans. \(-\frac{\sin (2 \ln x)}{x}\)

6. \(f(x)=\sqrt{3-\sqrt{x-2}}\) ফাংশনটির ডোমেন কত?
   1. \(x \leq 3\)
   2. \(x \geq 2\)
   3. \(2 \leq x \leq 11\)
   4. \(2 \leq x \leq 3\)

   Ans. \(2 \leq x \leq 11\)

7. \(\operatorname{cosec} \theta+\cot \theta=\sqrt{3}(0<\theta<\pi)\) হলে \(\theta\) এর মান হবে-
   1. \(\frac{\pi}{2}\)
   2. \(\frac{\pi}{3}\)
   3. \(\frac{\pi}{4}\)
   4. \(\frac{\pi}{6}\)

   Ans. \(\frac{\pi}{3}\)

8. যদি A, B, C ম্যাট্রিক্স তিনটির আকার যথাক্রমে \(4 \times 5,5 \times 4\) এবং \(4 \times 2\) হয়, তবে \(\left(A^{T}+B\right) C\) ম্যাট্রিক্সটির আকার কি?
   1. \(4 \times 2\)
   2. \(5 \times 4\)
   3. \(2 \times 5\)
   4. \(5 \times 2\)

   Ans. \(5 \times 2\)

9. পোলার স্থানাংকে \(r^{2}-2 r \sin \theta=3\) একটি বৃত্তের সমীকরণ। বৃত্তটির ব্যাসার্ধ হবে-
   1. 2
   2. 3
   3. 4
   4. 6

   Ans. 2

10. 3N ও 2N মানের দুইটি বলের লদ্বি R । প্রথম বলের মান দ্বিগুন করলে লদ্বির মানও দ্বিগুন হয়। বলদ্বয়ের মধ্যবর্তী কোণের মান হবে-
    1. \(30^{\circ}\)
    2. \(120^{\circ}\)
    3. \(65^{\circ}\)
    4. \(45^{\circ}\)

    Ans. \(120^{\circ}\)

11. 2u আদিবেগ এবং অনুভূমির সাথে লম্বভাবে প্রক্ষিপ্ত বস্তুর সর্ব্বোচ্চ উচ্চতা হবে-
    1. \(\frac{u^{2}}{2 g}\)
    2. \(\frac{2 u^{2}}{g}\)
    3. \(\frac{u^{2}}{2 g} \sin \alpha\)
    4. \(\frac{u^{2}}{2 g} \cos \alpha\)

    Ans. \(\frac{2 u^{2}}{g}\)

12. যদি \(y=k x(2 x+\sqrt{3})\) বক্ররেখার মূলবিন্দুতে স্পর্শকটি \(X\) অক্ষের সাথে \(30^{\circ}\) কোণ করে তাহলে K-এর মান কত হবে?
    1. \(\frac{1}{3}\)
    2. \(\sqrt{3}\)
    3. \(\frac{1}{\sqrt{3}}\)
    4. \(\frac{1}{2}\)

    Ans. \(\frac{1}{3}\)

13. \(x=a \cos \theta+b \sin \theta, y=a \sin \theta-b \cos \theta\) কোন কোনিকের সমীকরণ?
    1. ellipse
    2. parabola
    3. circle
    4. hyperbola

    Ans. circle

14. \(x^{2}-2 x+1=0\) সমীকরণটির মূলদ্বয়ের ত্রিঘাত এর সমষ্টি হলো-
    1. -3
    2. 3
    3. -2
    4. 2

    Ans. 2

15. \((1+x)^{7}(1-x)^{8}\) এর বিস্তৃতিতে \(x^{7}\) এর সহগ হলো-
    1. 15
    2. 30
    3. 25
    4. 35

    Ans. 35

গণিত (Mathematics) লিখিত অংশ

৯৷ \(x^{3}-3 x^{2}+7 x-5=0\) সমীকরণের একটি মূল \((1+2 i)\) হলে অন্য মূলগুলো নির্ণয় কর।

---

একটি মূল \((1+2 i)\) হলে অপর মূল \((1-2 i)\)
\((1+2 i)\) ও \((1-2 i)\) মূলবিশিষ্ট সমীকরণ,
\(x^2-2x+5=0\)
প্রদত্ত সমীকরণ,

\(x^{3}-3 x^{2}+7 x-5=0\)
বা, \(x^{3}-2 x^{2}+5x-x^{2}+2 x-5=0\)
বা, \(x(x^2-2x+5)-1(x^2-2x+5))=0\)
বা, \((x^2-2x+5)(x-1)=0\)
বা, \(x=1,1+2 i,1-2 i\)

---

১০৷ \(y=x^{2}\) এবং \(x=y^{2}\) দ্বারা সীমাবদ্ধ ক্ষেত্রের ক্ষেত্রফল নির্ণয় কর।

---

\(y=x^{2}\) এবং \(x=y^{2}\) হতে পাই,
\(x^4=x\)
বা, \(x^4-x=0\)
বা, \(x(x^3-1)=0\)
বা, \(x=0,1\)
ক্ষেত্রফল \(=\int\left(y_{1}-y_{2}\right) d x\)
\(=\int_{0}^{1}\left(x^{\frac{1}{2}}-x^{2}\right) d x\)
\(=\left[\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}-\frac{x^{2+1}}{2+1}\right]_{0}^{1}\)
\(=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}-\frac{x^{3}}{3}\right]_{0}^{1}\)
\(=\frac{2}{3}-\frac{1}{3}\)
\(=\frac{1}{3}\) বর্গ একক

---

১১। দেখাও যে, \(\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1} \frac{x+y}{1-x y}\)

---

\(\tan ^{-1} x=A \quad \therefore x=\tan A\)
\(\tan ^{-1} y=B \quad \therefore y=\tan B\)
\(\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}\)
    \(=\frac{x+y}{1-x y}\)
\(A+B=\tan ^{-1} \frac{x+y}{1-x y}\)
\(\therefore \tan ^{-1} x+\tan ^{-1} y=\tan ^{-1} \frac{x+y}{1-x y}\)

---

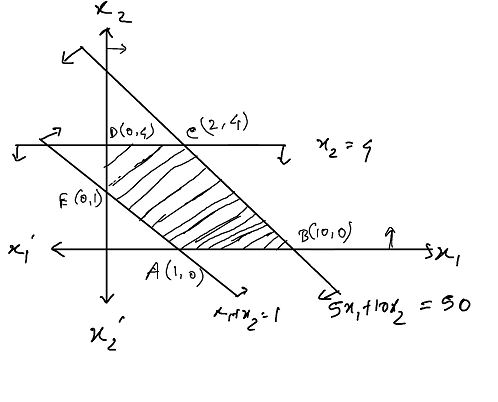
১২। \(5 x_{1}+10 x_{2} \leq 50, x_{1}+x_{2} \geq 1, x_{2} \leq 4, x_{1} \geq 0, x_{2} \geq 0\) শর্তাবলী সাপেক্ষে \(2 x_{1}+7 x_{2}\) এর লঘিষ্ঠ মান বের কর।

---

অসমতার অনুরূপ সমীকরণ,
\(\frac{x_{1}}{10}+\frac{x_{2}}{5}=1\)
\(\frac{x_{1}}{1}+\frac{x_{2}}{1}=1\)
\(x_{2}=4, x_{1}=0, x_{2}=0\)

\(Z_{A}=2(\min )\) Ans
\(Z_{B}=20\)
\(Z_{C}=32\)
\(Z_{D}=28\)
\(Z_{E}=7\)

জীববিজ্ঞান

1. দ্বৈত প্রচ্ছন্ন এপিস্টাসিস এর অনুপাত হলো-
   1. 3 : 1
   2. 2 : 1
   3. 13 : 3
   4. 9 : 7

   Ans. সাইকাস

2. নিচের কোনটিতে কোরালয়েড মূল পাওয়া যায়?
   1. Pinus
   2. Cycas
   3. Hibiscus
   4. Ficus

   Ans. ৯:৭

3. জলাভূমির উদ্ভিদ কোনটি?
   1. Barringtonia acutangula

   2. Tectona grandis

   3. Shorea robusta

   4. Caissia fistula

   Ans. Barringtonia acutangula

4. নিচের কোন এন্টিবডি বুকের দুধের মাধ্যমে প্রবাহিত হয়?
   1. IgA
   2. IgG
   3. IgM
   4. IgE

   Ans. IgA

5. পতঙ্গের সম্পূর্ণ রূপান্তর নিম্নলিখিত কোন ধাপগুলো নিয়ে গঠিত?
   1. ডিম-নিম্ফ-পূর্ণাঙ্গ-পতঙ্গ
   2. ডিম-লার্ভা-পিউপা-পূর্ণাঙ্গ-পতঙ্গ
   3. ডিম-লার্ভা-পূর্ণাঙ্গ-পতঙ্গ
   4. ডিম-পিউপা-লার্ভা-পূর্ণাঙ্গ-পতঙ্গ

   Ans. পূর্ণাঙ্গ পতঙ্গ

6. মানবদেহে স্টেম কোষ কোথায় পাওয়া যায়?
   1. অগ্ন্যাশয়ে
   2. যকৃতে
   3. অস্থিমজ্জায়
   4. হৃৎপিন্ডে

   Ans. অস্থিমজ্জায়

7. মানবদেহে কটিদেশীয় অঞ্চলে কশেরুকার সংখ্যা?
   1. ৪ টি
   2. ৭ টি
   3. ১২ টি
   4. ৫ টি

   Ans. ৫টি

8. চ্যাপ্টা কৃমির বৈজ্ঞানিক নাম কি?
   1. Faciola hepatica
   2. Loa loa
   3. Ascaris lumbricoides
   4. None of them

   Ans. Faciola hepatica

9. ম্যান্টল কোন পর্বের বৈশিষ্ট?
   1. Arthropoda
   2. Mollusca
   3. Annelida
   4. Echinodermata

   Ans. Mollusca

10. কোন ব্যাক্টেরিয়ায় একটি মাত্র ফ্লাজেলা থাকে?
    1. Vibrio cholerae
    2. Spirillum minus
    3. Pseudomonas fluorescens
    4. Bacillus subtilise

    Ans. Vibrio cholerae

11. উদ্ভিদের রোম অথবা ট্রাইকোম কোনটির অংশ?
    1. অধঃত্বক
    2. কর্টেক্স
    3. ত্বক
    4. অন্তঃত্বক

    Ans. ত্বক

12. নিচের কোনটিতে একিনিটি এবং হেটারোসিস্ট পাওয়া যায়?
    1. Escherichia
    2. Nostoc
    3. Zygnema
    4. Chlorella

    Ans. UGA

13. প্রোফেজ-১ এর কোন পর্যায়ে কায়াজমা সৃষ্টি হয়?
    1. লেপ্টেটিন
    2. জাইগোটিন
    3. ডিপ্লোটিন
    4. প্যাকাইটিন

    Ans. প্যাকাইটিন

14. মানবদেহে রক্তের প্লাজমার স্বাভাবিক pH কত?
    1. 7.0
    2. 7.6
    3. 7.8
    4. 7.4

    Ans. 7.4

15. কোন কোডনটি কোনো অ্যামাইনো অ্যাসিড নির্দেশ করে না?
    1. CCU
    2. ACU
    3. UGA
    4. AAG

    Ans. পুঞ্জীভূত

জীববিজ্ঞান (Biology) লিখিত অংশ

১৩। DNA প্রতিলিপন বলতে কী বুঝ? DNA প্রতিলিপনের জন্য প্রয়োজনীয় চারটি উপকরণের নাম লিখ।

---

ট্রান্সক্রিপশন: RNA পলিমারেজ এনজাইম দ্বারা DNA বেস সিকোয়েন্স কপি করে mRNA সংশ্লেষণ প্রক্রিয়া হলাে ট্রান্সক্রিপশন।
ট্রান্সক্রিপশন প্রক্রিয়ার জন্য যা প্রয়ােজন-

1. DNA ছাঁচ (template)
2. RNA-পলিমারেজ এনজাইম যা তিন প্রকার হতে পারে।
3. মুক্ত রাইবােনিউক্লিয়ােটাইড ট্রাইফসফেট (ATP, GTP, CTP এবং UTP)
4. রাসায়নিক শক্তি, ট্রাইফসফেট ভেঙ্গে নিউক্লিয়ােটাইড এবং পাইরােফসফেট সৃষ্টিকালে মুক্ত হয়।
   পাইরােফসফেট ভেঙ্গে দুই আয়ন ফসফেট তৈরি কালেও কিছু অতিরিক্ত শক্তি পাওয়া যায়।
5. কিছু সহযােগী প্রােটিন।

---

১৪। একবীজপত্রী উদ্ভিদের কাণ্ডের অন্তর্গঠনের পাঁচটি শনাক্তকারী বৈশিষ্ট্য লিখ।

---

একবীজপত্রী উদ্ভিদের কাণ্ডের অন্তর্গঠনের শনাক্তকারী বৈশিষ্ট্য:

• সাধারণত কান্ডরােম অনুপস্থিত।
• বহিঃত্বকে কিউটিকল উপস্থিত।
• অধঃত্বক আছে এবং সাধারণত ফ্লেরেনকাইমা টিস্যু দিয়ে গঠিত।
• ভাস্কুলার বান্ডলগুলাে গ্রাউন্ড টিস্যুতে বিক্ষিপ্তভাবে ছড়ানাে।
• মেটাজাইলেম পরিধির দিকে এবং প্রােটোজাইলেম কেন্দ্রের দিকে অবস্থিত।
• জাইলেম Y বা V আকৃতিবিশিষ্ট।
• ভাস্কুলার বান্ডল সংযুক্ত, সমপার্শ্বীয় ও বদ্ধ (জাইলেম ও ফ্লোয়েমের মাঝে ক্যাম্বিয়াম নেই)।

---

১৫৷ Platyhelminthes এবং Nemathelminthes এর পাঁচটি প্রধান পার্থক্য লিখ।

---

Platyhelminthes এবং Nemathelminthes এর পাঁচটি প্রধান পার্থক্য:

বিষয়	Platyhelminthes	Nemathelminthes
সাধারণ নাম	চ্যাপ্টা কৃমি	সুতাকৃমি বা গােলকৃমি
সংগঠন মাত্রা	টিস্যু-অঙ্গ মাত্রা	অঙ্গতন্ত্র মাত্রা
সিলােম	অ্যাসিলােমেট	সুডােসিলােমেট
যৌন দ্বিরূপতা।	অনুপস্থিত	উপস্থিত
শিখা কোষ	উপস্থিত	অনুপস্থিত
চোষক	উপস্থিত	অনুপস্থিত

---

১৬। মানবদেহের যে কোনো ১০টি করোটিকা স্নায়ুর নাম লিখ।

---

১০টি করােটিক স্নায়ুর নাম:

1. অলফ্যাক্টরি বা ঘ্রাণ গ্রহণকারী স্নায়ু।
2. অপটিক বা দর্শন স্নায়ু।
3. অকুলােমােটর
4. ট্রলিয়ার বা প্যাথেটিক স্নায়ু।
5. ট্রাইজেমিনাল
6. অ্যাবড়ুসেন্স।
7. ফ্যাসিয়াল।
8. অডিটরি বা ভেস্টিবুলাে ককলিয়ার স্নায়ু। |
9. গ্লসােফ্যারিঞ্জিয়াল
10. ভেগাস বা নিউমােগ্যাস্ট্রিক বা ক্ষুধার্ত স্নায়ু। |
11. অ্যাক্সেসরি।
12. হাইপােগ্লোসাল

বাংলা

1. “চিত্রময় বর্ণনার বাণী”- কবি কোথা থেকে কুড়িয়ে আনেন?
   1. প্রকৃতির ঐকতান স্রোত থেকে
   2. ভ্রমন বৃত্তান্ত থেকে
   3. মানষের কীর্তি থেকে
   4. কবিতা থেকে

   Ans. ভ্রমন বৃত্তান্ত থেকে

2. সালামের হাত থেকে কিসের মতো অবিনাশী বর্ণমালা ঝরে?
   1. কৃষ্ঞচূড়ার মত
   2. রক্তের বুদবুদের মত
   3. বিপ্লবের মত
   4. নক্ষত্রের মত

   Ans. নক্ষত্রের মত

3. স্থির শব্দের বিপরীত শব্দ হলো-
   1. জঙ্গম
   2. কোলাহল
   3. উচ্চরব
   4. নিশ্চল

   Ans. জঙ্গম

4. বেগম রোকেয়া সাখাওয়াত হোসেন সভ্যতার সঙ্গে দারিদ্র্য বৃদ্ধির কী কারণ নির্দেশ করেছেন?
   1. অলসতা
   2. বিলাসিতা
   3. অসততা
   4. অজ্ঞতা

   Ans. বিলাসিতা

5. কাজী নজরুল ইসলামের মতে, কিসের মধ্য দিয়ে সত্যকে পাওয়া যায়?
   1. মনুষ্যত্ব
   2. ধর্ম
   3. সংগ্রাম
   4. ভুল

   Ans. ভুল

6. বৃক্ষ কেবল বৃদ্ধির ইশারা নয়, মােতাহের হোসেন চৌধুরী বলেছেন, তা আরো কিছুর ইঙ্গিত; সেটি কী?
   1. বিবেচনাবোধ
   2. প্রশান্তি
   3. ধৈর্যশীলতা
   4. দ
      গতিময়তা

   Ans. প্রশান্তি

7. কোনটি পর্তুগিজ শব্দ নয়?
   1. আলপিন
   2. আলবোলা
   3. আলমারি
   4. আনারস

   Ans. আলবোলা

8. বিচার করে কাজ করে না যে, তাকে এককথায় বলে-
   1. অনুদার
   2. অশিক্ষিতপটু
   3. অবিমৃষ্যকারী
   4. অকুতোভয়

   Ans. অবিমৃষ্যকারী

9. নিচের কোনটি উত্তম পুরুষের ক্রিয়াপদের উদাহরণ?
   1. করেছ
   2. করেছি
   3. করেছিস
   4. করেছেন

   Ans. করেছি

10. ণ-ত্ব বিধান অনুসারে ভুল বানান আছে কোন গুচ্ছে?
    1. ধরন, পুরানো
    2. নেত্রকোনা, গৃহকোণ
    3. ক্ষণকাল, বর্ষণ
    4. মূল্যায়ণ, নিরূপন

    Ans. মূল্যায়ণ, নিরূপন

11. কোনটি অপপ্রয়োগ?
    1. একত্র
    2. একত্রিত
    3. একতাল
    4. একতা

    Ans. একত্রিত

12. ‘এবারের সংগ্রাম স্বাধীনতার সংগ্রাম’-এখানে কারক-বিভক্তি বিচারে স্বাধীনতার’ হলো-
    1. নিমিত্তার্থে ৬ষ্ঠী
    2. অপাদানে ৭মী
    3. নিমিত্তার্থে ৭মী
    4. কর্মে ৬ষ্ঠী

    Ans. নিমিত্তার্থে ৬ষ্ঠী

13. ‘অনাবৃষ্টির দিনে ফুলের কুড়ির মতো মেয়ের বিমর্ষ মুখ’। কোন রচনার বাক্য?
    1. রেইন কোট
    2. মহাজাগতিক কিউরেটর
    3. চাষার দুক্ষু
    4. অপরিচিতা

    Ans. অপরিচিতা

14. নিচের কোন কবিতায় ট্রয় নগরীর প্রসঙ্গ আছে?
    1. সাম্যবাদী
    2. সেই অস্ত্র
    3. ঐকতান
    4. বিভীষণের প্রতি মেঘনাদ

    Ans. সেই অস্ত্র

15. ‘সাম্যবাদী’ কবিতায় উল্লেখকৃত ‘জেন্দাবেস্তা’ কী?
    1. একপ্রকারের খাদ্য
    2. ধর্ম বিশেষ
    3. পারস্যের অগ্নি উপাসকদের ধর্মগ্রন্থ ও ভাষা
    4. উড়িষ্যার একটি স্থান

    Ans. পারস্যের অগ্নি উপাসকদের ধর্মগ্রন্থ ও ভাষা

বাংলা লিখিত অংশ

১৭। সারমর্ম লেখ (অনধিক চার বাক্যে):

তাই আমি মেনে নিই সে নিন্দার কথা
আমার সুরের অপূর্ণতা।
আমার কবিতা, জানি আমি
গেলেও বিচিত্র পথে হয় নাই সে সর্বত্রগামী।
কৃষাণের জীবনের শরিক যে জন,
কর্মে ও কথায় সত্য আত্মীয়তা করেছে অর্জন,
যে আছে মাটির কাছাকাছি,
সে কবির বাণী-লাগি কান পেতে আছি।

---

১৮। ভাব সম্প্রসারণ কর (অনধিক পাঁচটি বাক্যে):
এ বয়সে তাই নেই কোনো সংশয়
এ দেশের বুকে আঠারো আসুক নেমে।

---

১৯। ‘স্বাধীনতার সুবর্ণ জয়ন্তী’ নিয়ে পাঁচটি বাক্য লেখ।

---

২০। ‘নদী’ শব্দের পাঁচটি সমার্থ শব্দ লেখ।

---

ইংরেজি

Fill in the blank with the most appropriate option. (Questions 1-8)

1. ……………. his alert and vigilant presence, all predatory animals were said to have been kept within bounds.
   1. Hence
   2. However
   3. in addition to
   4. Because of

   Ans. Because of

2. Complete the following sentence using the most suitable options given below: “If had a car, … … …”
   1. I took you to a long drive
   2. I would have taken you to a long drive
   3. I would have been taken you to a long drive
   4. I would take you to a long drive

   Ans. I would take you to a long drive

3. Complete the sentence with the most appropriate option below. “The organization helps …………. elderly.”
   1. the
   2. an
   3. a
   4. no article

   Ans. the

4. Do you get ………. well ……… your sister?
   1. by, to
   2. on, with
   3. into, with
   4. in, to

   Ans. on, with

5. Do not make so much noise. Shibli ……….. to study for his admission test
   1. try
   2. tries
   3. tried
   4. is trying

   Ans. is trying

6. Would you mind …………… a cup of coffee with me?
   1. drink
   2. having to drink
   3. having
   4. to drink

   Ans. having

7. Bangladesh is ………….. huge inland open water resources.
   1. equipped with
   2. submerged by
   3. blessed by
   4. blessed with

   Ans. blessed with

8. By this time next year, I ……. all my exams.
   1. will taken
   2. have taken
   3. will have taken
   4. took

   Ans. will have taken

9. The synonym of ‘incompatible’ is-
   1. disqualified
   2. incomprehensible
   3. unsuitable
   4. incompetent

   Ans. unsuitable

10. If you are skeptical you are –
    1. credulous
    2. villainous
    3. philosophical
    4. doubtful

    Ans. doubtful

11. Change the voice of this sentence: “He does not like people laughing at him”.
    1. People laughing at him are not liked by him
    2. He does not like being laughed at.
    3. To be laughed at by people are not like by him
    4. He does not like him being laughed at by people.

    Ans. People laughing at him are not liked by him

12. The noun of ‘bore’ is –
    1. boring
    2. bores
    3. bored
    4. boredom

    Ans. boredom

13. Whose book is that?
    1. It’s of Mita’s.
    2. It’s Mitas’
    3. It’s Mita’s
    4. Its Mita’s

    Ans. It’s Mita’s

14. The antonym of ‘malign’ is-
    1. hostile
    2. bad
    3. benign
    4. harmful

    Ans. benign

15. Choose the correctly spelled word.
    1. Synonymus
    2. Hippopotamous
    3. Hypocrisy
    4. Antonymus

    Ans. Hypocrisy

English Written Part

২১। Write a short paragraph of 10 sentences on ‘The Dying Buriganga River’

---

২২। What is personification? Give an example of personification.

---

২৩।
“I love to rise in a summer morn,
When the birds sing on every tree;
The distant huntsman winds his horn,
O what sweet company!”
Which poem are these lines taken from? Who wrote this poem? What is the tone of the poem?

---

২৪। Write 10 sentences on how to minimize the chances of getting infected by the Corona Virus.

---