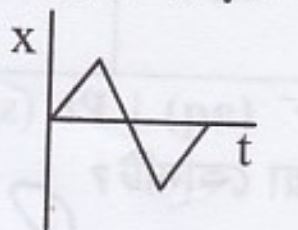DU A Unit Admission Question Solution 2019-2020

নিচের ভিডিওতে দেখে নাও বিস্তারিত:

কোর্সটি কিনতে পাশের বাটনটি ক্লিক কর:

কোর্সের ডেমো ভিডিও(এভাবে পদার্থবিজ্ঞান+রসায়ন+উচ্চতরগণিত এর বিগত বিশ বছরের সকল প্রশ্নের সমাধান থাকবে ভিডিওতে)

পদার্থবিজ্ঞান

দুইটি ভেক্টর \(\overrightarrow{\mathbf{A}}=3 \hat{\mathbf{i}}-3 \hat{\mathbf{j}}\) এবং \(\overrightarrow{\mathbf{B}}=5 \hat{\mathbf{i}}+5 \hat{\mathbf{k}}\) এর মধ্যবর্তী কোণ কত?
1. \(60^{\circ}\)
2. \(30^{\circ}\)
3. \(45^{\circ}\)
4. \(90^{\circ}\)
Ans. \(60^{\circ}\)
স্থির অবস্থায় থাকা একটি বস্তু বিস্ফোরিত হয়ে \(\mathrm{m}_{1}\) ও \(\mathbf{m}_{2}\) ভরের
দুইটি বস্তুতে পরিণত হয়ে যথাক্রমে \(\mathbf{v}_{\mathbf{1}}\) ও \(\mathbf{v}_{2}\) বেগে বিপরীত দিকে চলমান। \(\frac{\mathbf{v}_{\mathbf{1}}}{\mathbf{v}_{\mathbf{2}}}\) এর অনুপাত কত?
1. \(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}\)
2. \(-\frac{m_{1}}{m_{2}}\)
3. \(\frac{\mathrm{m}_{2}}{\mathrm{~m}_{1}}\)
4. \(\sqrt{\frac{\mathrm{m}_{2}}{\mathrm{~m}_{1}}}\)
Ans. \(\frac{\mathrm{m}_{2}}{\mathrm{~m}_{1}}\)
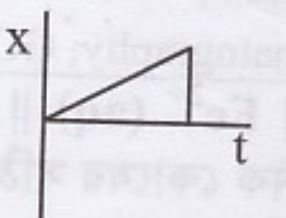
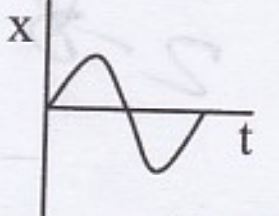
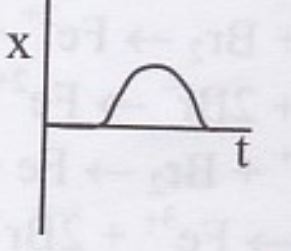
একটি গাড়ি স্থির অবস্থা (P বিন্দু) হতে সোজা রাস্তায় যাত্রা
শুরু করল। কিছু সময় পরে গাড়িটি মন্দনের ফলে থেমে গেল এবং একই ভাবে (প্রথম গতি বাড়িয়ে এবং পরে গতি কমিয়ে) আবার যাত্রা শুরু করে P বিন্দুতে ফিরে আসলো। নিচের কোন লেখচিত্রটি গাড়ির গতিকে প্রকাশ করে?
Ans.
নিচের কোনটি ভরের একক নয়?
1. a.m.u
2. \(\mathrm{Nm}^{-1} \mathrm{~s}^{2}\)
3. \(\mathrm{MeV}\)
4. \(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\)
Ans. \(\mathrm{MeV}\)
সরল ছন্দিত গতিতে স্পন্দনরত দুটি কণার সরণ \(\mathbf{x}_{1}=\mathbf{A} \sin \omega \mathbf{t}\)
এবং \(\mathbf{x}_{\mathbf{2}}=\mathbf{A} \cos \omega \mathbf{t}\) যে কোনো সময়ে এদের মধ্যে দশা পার্থক্য কত হবে?
1. \(2 \pi\)
2. \(\pi\)
3. \(\frac{\pi}{2}\)
4. \(\frac{\pi}{4}\)
Ans. \(\frac{\pi}{2}\)
ব্যতিচারের ক্ষেত্রে উজ্জ্বল বা গঠনমূলক ঝালরের শর্ত কোনটি?
1. \(\sin \theta=(2 n+1) \frac{\lambda}{2}\)
2. a \(\sin \theta=n \lambda\)
3. \(\sin \theta=n \frac{\lambda}{2}\)
4. \(a \sin \theta=(2 n+1) \lambda\)
Ans. a \(\sin \theta=n \lambda\)
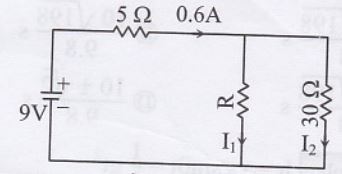
নিচের বর্তনীতে তড়িৎপ্রবাহ \(\mathbf{I}_{\mathbf{1}}\) এর মান কত?
1. \(0.2 \mathrm{~A}\)
2. \(0.4 \mathrm{~A}\)
3. \(0.6 \mathrm{~A}\)
4. \(1.2 \mathrm{~A}\)
Ans. \(0.4 \mathrm{~A}\)
একটি কার্নো ইঞ্জিন 500 K এবং 250 k তাপমাত্রার আধারের
মাধ্যমে পরিচালিত হয়। প্রত্যেক চক্রে ইঞ্জিন যদি উৎস থেকে 1kcal তাপ গ্রহণ করে তাহলে প্রত্যেক চক্রে তাপ গ্রাহকে তাপ বর্জন করার পরিমাণ কত?
1. 500 kcal
2. 1000 cal
3. 500 cal
4. 10 kcal
Ans. 500 cal
q পরিমাণ আধান একটি চৌম্বক ক্ষেত্র \(\overrightarrow{\mathbf{B}}\) এর সাথে সমান্তরালে
\(\overrightarrow{\mathbf{v}}\) বেগে গতিশীল। উক্ত স্থানে একটি তড়িৎক্ষেত্র \(\overrightarrow{\mathbf{E}}\) থাকলে আধানের উপর ক্রিয়াশীল বল কত হবে?
1. \(\mathrm{q}(\overrightarrow{\mathrm{E}}+\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})\)
2. \(\mathrm{q}(\overrightarrow{\mathrm{E}}+\overrightarrow{\mathrm{v}} \cdot \overrightarrow{\mathrm{B}})\)
3. \(\mathrm{q} \overrightarrow{\mathrm{E}}\)
4. \(q(\vec{E}+\vec{B})\)
Ans. \(\mathrm{q} \overrightarrow{\mathrm{E}}\)
কাগজের ভার হিসাবে ব্যবহৃত একটি পুরু কাচ (প্রতিসরাঙ্ক
1.5) খণ্ডের উপর থেকে খাড়া নিচের দিকে তাকালে কাগজের উপর একটি দাগ কাচের উপর প্রান্ত থেকে 6 cm নিচে দেখা যায়। কাচ খণ্ডটির পুরুত্ব কত?
1. 4 cm
2. 6 cm
3. 9 cm
4. 12 cm
Ans. 9 cm
একটি বস্তু \(\pi \mathrm{m}\) ব্যাসার্ধের বৃত্তাকার পথে \(4.0 \mathrm{~m} / \mathrm{s}\) সমদ্রুতিতে
ঘুরছে। একবার ঘুরে আসতে বস্তুটির কত সময় লাগবে?
1. \(2 / \pi^{2} \mathrm{~s}\)
2. \(\pi^{2} / 2 \mathrm{~s}\)
3. \(\pi / 2 \mathrm{~s}\)
4. \(\pi^{2} / 4 \mathrm{~s}\)
Ans. \(\pi^{2} / 2 \mathrm{~s}\)
5 m উচ্চতা হতে একটি বলকে 20 m/s বেগে অনুভূমিকের সাথে
30° কোণে উপরের দিকে নিক্ষেপ করা হলো। তাহলে বলটির বিচরণকাল কত?
1. \(\frac{10+\sqrt{198}}{9.8} \mathrm{~s}\)
2. \(\frac{10 \sqrt{198}}{9.8} \mathrm{~s}\)
3. \(\frac{10 \pm \sqrt{198}}{9.8} \mathrm{~s}\)
4. \(\frac{10 \pm \sqrt{2}}{9.8} \mathrm{~s}\)
Ans. \(\frac{10+\sqrt{198}}{9.8} \mathrm{~s}\)
10 cm লম্বা ও 0.5 cm ব্যাসার্ধ বিশিষ্ট একটি তামা ও একটি
লোহার তারকে জোড়া লাগিয়ে দৈর্ঘ্য 20 cm করা হলো। জোড়া লাগানো তারটিকে বল প্রয়োগ করে লম্বা করা হলো। লোহার ইয়ং-এর গুণাঙ্ক তামার ইয়ংয়ের গুণাঙ্কের দুইগুণ হলে লোহার দৈর্ঘ্য বৃদ্ধি ও তামার দৈর্ঘ্য বৃদ্ধির অনুপাত কত?
1. 1:8
2. 1:6
3. 1:4
4. 1:2
Ans. 1:2
একটি স্থির তরঙ্গে পরপর দুটি নিস্পন্দ বিন্দুর মধ্যবর্তী দূরত্ব 1m, এর তরঙ্গদৈর্ঘ্য কত?
1. 25 cm
2. 50 cm
3. 100 cm
4. 200 cm
Ans. 200 cm
অ্যালুমিনিয়াম, হিলিয়াম এবং সিলিকনের পারমাণবিক সংখ্যা যথাক্রমে 13, 2 এবং 14 হলে, \(_{13} \mathbf{A l}^{27}+_{2}\mathbf{H e}^{4} \rightarrow _{14}\mathbf{S i}^{28}+()\) নিউক্লিয়ার বিক্রিয়াতে অনুপস্থিত কণা কোনটি?
1. an \(\alpha\) particle
2. an electron
3. a positron
4. a proton
Ans. প্রশ্নটি ভুল আছে।

রসায়ন

প্রোটিন অণুর মধ্যে অ্যামাইনো এসিডের অণুসমূহ যে বন্ধন দ্বারা
যুক্ত থাকে-
1. Glycosidic bond
2. Peptide bond
3. Hydrogen bond
4. Metallic bond
Ans. Peptide bond
নিম্নের কোনটিকে সাধারণত তরল-তরল ক্রোমাটোগ্রাফি বলে?
1. গ্যাস ক্রোমাটোগ্রাফি
2. কাগজ ক্রোমাটোগ্রাফি
3. কলাম ক্রোমাটোগ্রাফি
4. পাতলা স্তর ক্রোমাটোগ্রাফি
Ans. কাগজ ক্রোমাটোগ্রাফি
\(\mathrm{Fe}(\mathrm{s})\left|\mathrm{Fe}^{\mathrm{2}^{+}}(\mathrm{aq}) \| \mathrm{Br}_{2}(l) ; \mathrm{Br}^{-}(\mathrm{aq})\right| \mathrm{Pt}(\mathrm{s})\) তড়িৎ
রাসায়নিক কোষের সঠিক কোষ-বিক্রিয়া কোনটি?
1. \(\mathrm{Fe}+\mathrm{Br}_{2} \rightarrow \mathrm{Fe}^{2+}+2 \mathrm{Br}^{-}\)
2. \(\mathrm{Fe}+2 \mathrm{Br}^{-} \rightarrow \mathrm{Fe}^{2+}+\mathrm{Br}_{2}\)
3. \(\mathrm{Fe}^{2+}+\mathrm{Br}_{2} \rightarrow \mathrm{Fe}+2 \mathrm{Br}^{-}\)
4. \(\mathrm{Fe} \rightarrow \mathrm{Fe}^{3+}+2 \mathrm{Br}^{-}\)
Ans. \(\mathrm{Fe}+\mathrm{Br}_{2} \rightarrow \mathrm{Fe}^{2+}+2 \mathrm{Br}^{-}\)
নিম্নের কোন যৌগটি জ্যামিতিক সমাণুতা প্রদর্শন করে?
1. \(\left(\mathrm{CH}_{3}\right)_{3} \mathrm{~N}\)
2. \(\mathrm{CH}_{3} \mathrm{CH}=\mathrm{CH}_{2}\)
3. \(\left(\mathrm{CH}_{5}\right)_{2} \mathrm{NH}\)
4. \(\mathrm{CH}_{3} \mathrm{CH}=\mathrm{CHCH}_{3}\)
Ans. \(\mathrm{CH}_{3} \mathrm{CH}=\mathrm{CHCH}_{3}\)
আর্দ্র বাতাসের সংস্পর্শে ক্যালসিয়াম কার্বাইড নিম্নের কোন যৌগটি
উৎপন্ন করে?
1. Ethanal
2. Ethane
3. Ethyne
4. Ethene
Ans. Ethyne
উত্তেজিত অবস্থায় হাইড্রোজেন পরমাণুর কোয়ান্টাম সংখ্যা
n = 4,l= 1 বিশিষ্ট অরবিটালটি কি?
1. s orbital
2. p orbital
3. \(\mathrm{d}_{\mathrm{Z}}^{2}\) orbital
4. \(\mathrm{d}_{\mathrm{x}}^{2}-\mathrm{y}^{2}\) orbital
Ans. p orbital
\(\mathrm{CH}_{3}-\mathrm{CH}\left(\mathrm{C}_{2} \mathrm{H}_{5}\right)-\mathrm{CH}_{2}-\mathrm{CHBr}-\mathrm{CHCl}-\mathrm{CH}_{3}\)যৌগটির IUPAC নাম হলো-
1. 2-ক্লোরো-3-ব্রোমো-5-ইথাইলহেক্সেন
2. 2-ক্লোরো-3-ব্রোমো-5-মিথাইলহেপটেন
3. 3-ব্রোমো-2-ক্লোরো-5-ইথাইলহেক্সেন
4. 3-ব্রোমো-2-ক্লোরো-5-মিথাইলহেপটেন
Ans. 3-ব্রোমো-2-ক্লোরো-5-মিথাইলহেপটেন
কার্বন মৌল হীরা ও গ্রাফাইট-এ ভিন্নরূপ। এদের ক্ষেত্রে কোন উক্তিটি
সত্য নয়?
1. উভয়েই কার্বন মৌল দ্বারা গঠিত।
2. হীরা ও গ্রাফাইটে কার্বন পরমাণুর সংকরায়ন হলো যথাক্রমে \(\mathrm{sp}^{3}\) ও \(\mathrm{sp}^{2}\)
3. উভয়ের বিদ্যুৎ পরিবাহিতা ভিন্ন।
4. উভয়ের দহন তাপ একই।
Ans. উভয়ের দহন তাপ একই।
MRI যন্ত্রের সাহায্যে মানবদেহের রোগ নির্ণয়ে কোন মৌলটির
ভূমিকা রয়েছে?
1. Neon
2. Oxygen
3. Hydrogen
4. Silicon
Ans. Hydrogen
নিম্নের কোন পরীক্ষাটি সালফিউরিক এসিড ও নাইট্রিক
এসিডের মধ্যে পার্থক্য করতে ব্যবহার করা যায়?
1. সার্বজনীন নির্দেশক দিয়ে পরীক্ষা
2. সোডিয়াম কার্বনেট গুঁড়া যোগে।
3. ম্যাগনেশিয়াম ফিতা যোগে।
4. বেরিয়াম নাইট্রেট দ্রবণ যোগে।
Ans. বেরিয়াম নাইট্রেট দ্রবণ যোগে।
নাইট্রেট অ্যানায়নে কয়টি ইলেকট্রন রয়েছে?
1. 19
2. 31
3. 23
4. 32
Ans. 32
50 mL তরল পরিমাপ করতে নিম্নের কোনটির ব্যবহার যথার্থ?
1. পিপেট
2. মাপন সিলিন্ডার
3. বুরেট
4. আয়তনিক ফ্লাক্স
Ans. মাপন সিলিন্ডার
0.98g \(\mathrm{H}_{2} \mathrm{SO}_{4}\) ব্যবহার করে 1.0L জলীয় দ্রবণ তৈরি করা হলে। দ্রবণটির ঘনমাত্রা কত?
1. 0.1 M
2. 0.1 m
3. 0.01 M
4. 0.01 m
Ans. 0.01 M
\(\mathrm{BaMnF}_{4}\) এবং \(\mathrm{Li}_{2} \mathrm{MgFeF}_{6}\) যৌগদ্বয়ে Mn ও Fe এর জারণ
সংখ্যা যথাক্রমে-
1. +2,+2
2. +5,+2
3. +4,+3
4. +5,+3
Ans. +2,+2
কোনটি অম্লীয় জলীয় দ্রবণ তৈরি করে?
1. \(\mathrm{Na}_{2} \mathrm{O}\)
2. \(\mathrm{ZnO}\)
3. \(\mathrm{Al}_{2} \mathrm{O}_{3}\)
4. \(\mathrm{CO}_{2}\)
Ans. \(\mathrm{CO}_{2}\)

উচ্চতর গণিত

\(A=\left(\begin{array}{ll}3 & -4 \\ 2 & -3\end{array}\right)\) হলে, \(\operatorname{det}\left(2 \mathrm{~A}^{-1}\right)\) এর মান হলো –
1. \(\frac{1}{4}\)
2. \(-4\)
3. \(4\)
4. \(-\frac{1}{4}\)
Ans. \(-4\)
যদি \(f(x)=x^{2}-2|x|\) এবং \(g(x)=x^{2}+1\) হয়, তাহলে \(g(f(-2))\)
এর মান কত?
1. 0
2. 1
3. -1
4. 5
Ans. 1
\(\frac{1+i}{1-i}\) এর পরম মান হলো-
1. 0
2. 1
3. \(\sqrt{2}\)
4. i
Ans. 1
\(\underset {x \rightarrow -\infty} {\overset { } {\mathrm lim} } \frac{\sqrt{x^{2}+2 x}}{-x}\) এর মান হলো-
1. 1
2. \(\infty\)
3. \(-\infty\)
4. -1
Ans. -1
(4, 3) কেন্দ্রবিশিষ্ট এবং 5x – 12y + 3 = 0 সরলরেখাকে
স্পর্শ করে এমন বৃত্তের সমীকরণ কোনটি?
1. \(x^{2}+y^{2}+8 x-6 y+24=0\)
2. \(x^{2}+y^{2}-8 x-6 y+24=0\)
3. \(x^{2}+y^{2}+8 x+6 y+24=0\)
4. \(x^{2}+y^{2}-8 x-6 y-24=0\)
Ans. \(x^{2}+y^{2}-8 x-6 y+24=0\)
\(\overrightarrow{\mathbf{b}}=6 \hat{\mathbf{i}}+7 \hat{\mathbf{j}}-6 \hat{k}\) ভেক্টর বরাবর \(\overrightarrow{\mathbf{a}}=\mathbf{2} \hat{\mathbf{i}}-\mathbf{2} \hat{\mathbf{j}}+\hat{\mathbf{k}}\) ভেক্টরের
উপাংশ হলো-
1. \(\frac{8}{121} \overrightarrow{\mathrm{b}}\)
2. \(\frac{-8}{121} \overrightarrow{\mathrm{b}}\)
3. \(\frac{8}{121} \overrightarrow{\mathrm{a}}\)
4. \(\frac{-8}{121} \vec{a}\)
Ans. \(\frac{-8}{121} \overrightarrow{\mathrm{b}}\)
‘GEOMETRY’ শব্দটির বর্ণগুলোর সবগুলো একত্রে নিয়ে।
কত প্রকারে সাজানো যায় যেন প্রথম ও শেষ অক্ষর ‘E’ থাকে?
1. 360
2. 20160
3. 720
4. 30
Ans. 720
\(\left(2 x+\frac{1}{8 x}\right)^{8}\) এর বিস্তৃতিতে x বর্জিত পদের মান হলো-
1. \(\frac{70}{81}\)
2. 520
3. \(\frac{35}{128}\)
4. \(\frac{7}{512}\)
Ans. \(\frac{35}{128}\)
\(25 x^{2}+16 y^{2}=400\) উপবৃত্তের উৎকেন্দ্রিকতা কত?
1. \(\frac{2}{3}\)
2. \(\frac{4}{5}\)
3. \(\frac{3}{4}\)
4. \(\frac{3}{5}\)
Ans. \(\frac{3}{5}\)
\(\cot \left(\sin ^{-1} \frac{1}{2}\right)=?\)
1. \(\frac{1}{\sqrt{3}}\)
2. \(\frac{\sqrt{3}}{2}\)
3. \(\sqrt{3}\)
4. \(\frac{2}{\sqrt{3}}\)
Ans. \(\sqrt{3}\)
[0, 2] ব্যবধিতে \(y=x-1\) এবং \(\mathbf{y}=\mathbf{0}\) রেখা দ্বারা আবদ্ধ
অঞ্চলের মোট ক্ষেত্রফল কত?
1. \(\int_{0}^{2}(x-1) d x\)
2. \(\int_{0}^{2}|x-1| d x\)
3. \(2 \int_{1}^{2}(1-x) d x\)
4. \(2 \int_{0}^{1}(x-1) d x\)
Ans. \(2 \int_{0}^{1}(x-1) d x\)
\(\frac{1}{|3 x-1|}>1\) এর সমাধান হলো-
1. \(\left(-\infty, \frac{1}{3}\right) \cup(1, \infty)\)
2. \(x>\frac{1}{3}\)
3. \(0< x<\frac{2}{3}\)
4. \(\left(0, \frac{1}{3}\right) \cup\left(\frac{1}{3}, \frac{2}{3}\right)\)
Ans. \(\left(0, \frac{1}{3}\right) \cup\left(\frac{1}{3}, \frac{2}{3}\right)\)
\(\int \frac{d x}{\left(e^{x}+e^{-x}\right)^{2}}=?\)
1. \(\frac{1}{2\left(\mathrm{e}^{2 \mathrm{x}}+1\right)}+\mathrm{c}\)
2. \(\frac{-1}{2\left(\mathrm{e}^{2 \mathrm{x}}+1\right)}+\mathrm{c}\)
3. \(\frac{1}{2 e^{2 x}}+c\)
4. \(\frac{-1}{2 e^{2 x}}+c\)
Ans. \(\frac{-1}{2\left(\mathrm{e}^{2 \mathrm{x}}+1\right)}+\mathrm{c}\)
\(f(x)=\sqrt{2-\sqrt{2-x}}\) এর ডোমেইন হলো-
1. \((-\infty, 2)\)
2. \((-\infty, \infty)\)
3. \((-2, \infty)\)
4. \([-2,2]\)
Ans. \([-2,2]\)
কোনো একটি বিন্দুতে ক্রিয়ারত \(\overrightarrow{\mathbf{p}}\) ও \(2 \overrightarrow{\mathbf{p}}\) বলদ্বয়ের লব্ধি \(\sqrt{7} \overrightarrow{\mathbf{p}}\)
হলে, তাদের মধ্যবর্তী কোণ কত?
1. 30°
2. 90°
3. 60°
4. 180°
Ans. 60°

জীববিজ্ঞান

পনির তৈরিতে ব্যবহৃত এনজাইমের নাম-
1. পেপেইন
2. রেনিন
3. ক্যাটালেজ
4. পেকটিন
Ans. রেনিন
শিখাকোষ যে পর্বের বৈশিষ্ট্য?
1. আথ্রোপোডা
2. অ্যানিলিডা
3. মলাস্কা
4. প্লাটিহেলমিনথেস
Ans. প্লাটিহেলমিনথেস
মানবদেহে ইমিউনোগ্লোবিনের কত ভাগ IgG?
1. 75%
2. 15%
3. 10%
4. 5%
Ans. 75%
কোনটি পত্রঝরা উদ্ভিদ?
1. Pongamia pinnat
2. Heritiera fomes
3. Shorea robusta
4. Ceriops decandra
Ans. Shorea robusta
কোন হরমোনের উৎস পিটুইটারি গ্রন্থি নয়?
1. ভ্যাসোপ্রেসিন
2. প্রোজেস্টেরন
3. প্রোলাক্টিন
4. অক্সিটসিন
Ans. প্রোজেস্টেরন
মানব জিনোমে ক্ষারক-যুগলের সংখ্যা-
1. ৩ মিলিয়ন
2. ৩০ মিলিয়ন
3. ৩০০ মিলিয়ন
4. ৩০০০ মিলিয়ন
Ans. ৩০০০ মিলিয়ন
কোন অ্যামাইনো এসিডের জন্য ৪টি কোড রয়েছে?
1. লিউসিন
2. আরজিনিন
3. ভ্যালিন
4. ট্রিপটোফেন
Ans. ভ্যালিন
কোন উদ্ভিদটি বাংলাদেশে বিলুপ্তপ্রায়?
1. Pteris vittata
2. Podocarpus nerifolia
3. Cycas revoluta
4. Nerium indicum
Ans. Podocarpus nerifolia
কোন অঙ্গাণুতে অক্সিসোম দেখা যায়?
1. মাইটোকন্ড্রিয়া
2. নিউক্লিয়াস
3. রাইবোসোম
4. লাইসোসোম
Ans. মাইটোকন্ড্রিয়া
Poaceae গোত্রের উদ্ভিদের ফলকে বলা হয়-
1. বেরি
2. ক্যারিওপসিস
3. পড
4. ক্যাপসুল
Ans. ক্যারিওপসিস
মানুষের মস্তিষ্ক ও সুষুম্নাকাণ্ডের আবরণ কোনটি?
1. মেনিনজেস
2. পেরিটোনিয়াম
3. পেরিকারডিয়াম
4. নিউরোকারডিয়াম
Ans. মেনিনজেস
কোন প্রাণীতে প্ল্যাকয়েড আঁশ রয়েছে?
1. হাঙর
2. তারামাছ
3. কইমাছ
4. কাতল মাছ
Ans. হাঙর
অ্যাড্রেনাল গ্রন্থি থেকে কোন হরমোন নিঃসৃত হয়?
1. গুকোকরটিকয়েড
2. গোনাডোট্রপিন
3. প্যারাথরমোন
4. ক্যালসিটনিন
Ans. গুকোকরটিকয়েড
কোনটির পরিবহনতন্ত্র আছে, কিন্তু ফুল হয় না?
1. থ্যালোফাইটা
2. ব্রায়োফাইটা
3. টেরিডোফাইটা
4. স্পারমাটোফাইটা
Ans. টেরিডোফাইটা।
পলিজিন এর প্রভাব-
1. সমপ্রকট
2. প্রকট
3. প্রচ্ছন্ন
4. পুঞ্জীভূত
Ans. পুঞ্জীভূত

বাংলা

‘আজব’ শব্দটি কোন বিদেশি শব্দ?
1. আরবি
2. ফরাসি
3. হিন্দি
4. উর্দু
Ans. আরবি
ণ-ত্ব বিধান অনুযায়ী কোনটি অশুদ্ধ?
1. দুর্ণীতি
2. দারুণ
3. মূল্যায়ন
4. বর্ণ
Ans. দুর্ণীতি
‘মাসি-পিসি’ গল্পে আহ্লাদির মুখে কে দেখতে পায় নিজ মেয়ের মুখের ছাপ?
1. কৈলেশ
2. জগু
3. রহমান
4. কানাই
Ans. রহমান
‘বিভীষণের প্রতি মেঘনাদ’ কবিতায় কাকে বাসবত্রাস বলা
হয়েছে?
1. বিভীষণকে
2. রামকে
3. রাবণকে
4. মেঘনাদকে
Ans. মেঘনাদকে
‘সমুদ্র’ শব্দটির প্রতিশব্দ-
1. রত্নাকর
2. অম্বুজ
3. জলদ
4. বরুণ
Ans. রত্নাকর।
‘নৈয়ায়িক’ কাকে বলা হয়?
1. নীতিবানকে
2. যিনি ন্যায়শাস্ত্র জানেন
3. পণ্ডিতকে
4. তার্কিককে
Ans. যিনি ন্যায়শাস্ত্র জানেন
কোন শব্দগুচ্ছ শুদ্ধ?
1. সমীচীন, কণ্ঠ, মাষ্টার
2. অঙ্গুলি, দন্ডনীয়, কিংকর্তব্যবিমুঢ়
3. প্রতিযোগিতা, স্বাদেশীক, সন্তরণ
4. সহযোগী, শিরচ্ছেদ, গুঞ্জরন
Ans. সহযোগী, শিরচ্ছেদ, গুঞ্জরন
‘বৈশিষ্ট্য’ শব্দটি গঠিত হয়েছে-
1. সন্ধিযোগে
2. সমাসযোগে
3. প্রত্যয়যোগে
4. উপসর্গযোগে
Ans. প্রত্যয়যোগে
‘আঠারো বছর বয়স’ কবিতার মূলসুর?
1. নৈতিকতা
2. বিবেকবোধ
3. অদম্য তারুণ্যশক্তি
4. ভীরুতা
Ans. অদম্য তারুণ্যশক্তি
কোনটি ধ্বন্যাত্মক শব্দের উদাহরণ?
1. শীত-শীত
2. ঘুম-ঘুম
3. জ্বরজ্বর
4. টুপটাপ
Ans. টুপটাপ
কোন উপসর্গটি ভিন্নার্থে প্রযুক্ত?
1. প্রতিপক্ষ
2. প্রতিদ্বন্দ্বী
3. প্রতিবিম্ব
4. প্রতিবাদ
Ans. প্রতিবিম্ব
‘তোমার কথাগুলি ভারি সোশিয়ালিস্টিক’। এ উক্তি কার
উদ্দেশে উচ্চারিত হয়েছে?
1. কমলাকান্ত
2. বঙ্কিমচন্দ্র
3. মার্জার
4. প্রসন্ন
Ans. মার্জার
কারমাইকেলের অনুসন্ধানে রেশমি রুমাল তৈরির ক্ষেত্র হিসেবে
কোন এলাকা আবিষ্কৃত হয়েছে?
1. বীরভূম
2. বর্ধমান
3. রাজশাহী
4. মুর্শিদাবাদ
Ans. মুর্শিদাবাদ
কোনটি অপপ্রয়োগের দৃষ্টান্ত?
1. পুনঃপুন
2. ভৌগলিক
3. গ্রথিত
4. প্রোথিত
Ans. ভৌগলিক
‘আমার পথ’ প্রবন্ধে পথপ্রদর্শক কে?
1. ধর্ম
2. সত্য
3. দেশ
4. নেতা
Ans. সত্য

ইংরেজি

English Read the following passage and answer the questions (1-5)
‘Bacteria’ is the common name of a very large group of one-celled microscopic organism that, we believe, may be the smallest, simplest and perhaps even the very first form of cellular life that evolved on earth. That is why they are observable only under a microscope. There are three main types of bacteria, which are classified according to their shape.
The bacilli are a group of bacteria that occur in the soil and air. They are shaped like rods. If we look at them under a microscope, we find them in motion, they always seem to be rolling or tumbling under the microscope. These bacilli are largely responsible for food spoilage. There is another group of bacteria who tend to grow in chains. They are referred to as the cocci group. A common example of this type is streptococci that causes strep throat. Finally, there is the spiral shaped bacteria called. They look a little like corkscrews, and they are responsible for a number of diseases in humans. Some species of bacteria cause diseases, but mostly bacteria live harmlessly on the skin, in the mouth, and the intestines. In fact, bacteria are very helpful to researchers. Bacteria cells resemble the cells of other life forms in many ways, and may be studied to give us insights.

Which is the topic of this passage?
1. Three major types of bacteria
2. How microscopic organisms are mesured
3. How bacteria is used for research in genetics
4. Diseases caused by bacteria
Ans. Three major types of bacteria
A similar word for ‘tumble’is —
1. order
2. arrange
3. organize
4. spill
Ans. spill
According to the passage, bacilli are responsible for –
1. polluting air
2. causing throat diseases
3. spoilling food
4. spoilling soil
Ans. spoilling food
According to the text, which characteristic is common
in bacteria?
1. They have one cell
2. They are harmful to humans
3. They die quickly
4. They die when exposed to air
Ans. They have one cell
Why are bacteria used in the research study?
1. Bacteria live harmlessly
2. Bacteria are similar to other life forms
3. Bacteria cause many diseases
4. Bacteria have cell formations
Ans. Bacteria are similar to other life forms

Fill in each blank with appropriate word/words
(Question 6 -15)

Nutritionists still do not understand the nutritional _____
of jackfruits.
1. favours
2. helps
3. goods
4. benefits
Ans. benefits
A synonym for ‘compassion’ is _____
1. indifference
2. cruelty
3. yearning
4. heartlessness
Ans. yearning
As for _____, I prefer to let people make up _____ minds.
1. myself, each other’s
2. me, their own
3. my, theirs
4. mine, one another
Ans. me, their own
The noun of ‘excite’ is-
1. excitable
2. exciting
3. excited
4. excitement
Ans. excitement
Kalam found it hard to get up from bed after the alarm
clock _____ at six a.m.
1. sent out
2. threw out
3. went off
4. took out
Ans. went off
Which one is the incorrect spelling?
1. deportation
2. depriciation
3. denunciation
4. denomination
Ans. depriciation
What is the antonym of ‘latent’?
1. lurking
2. hidden
3. obvious
4. concealed
Ans. obvious
Monir is sitting ______ the desk _____ front of the door.
1. at, in
2. in, on
3. on, on
4. at, at
Ans. at, in
Sleeplessness causes problems with our _____ clock.
1. botanical
2. biological
3. natural
4. rhythmical
Ans. biological
The person who has committed such an _____ crime must
be severely punished.
1. injurious
2. unworthy
3. uncharitable
4. abominable
Ans. abominable

লিখিত অংশ (১১.২৫ x ৪ = ৪৫)

পদার্থবিজ্ঞান

প্রশ্ন-01. সমবেগে চলন্ত 2500 kg ভরের একটি গাড়ি মন্দনের ফলে
2500 m দূরত্ব অতিক্রম করার পর থেমে গেল। গাড়িটি থামানোর জন্য প্রদত্ত বল এবং থামার সময় নির্ণয় কর।

সমাধান:

\(v^{2}=u^{2}-2 a s\)
\(\Rightarrow 0=(50)^{2}-2 \times \mathrm{a} \times 2500\)
\(\Rightarrow \mathrm{a}=0.5 \mathrm{~ms}^{-2}\)
\(\therefore \mathrm{v}=\mathrm{u}-\mathrm{at}\)
\(\Rightarrow 0=50-0.5 \times \mathrm{t}\)
\(\Rightarrow \mathrm{t}=100 \mathrm{~s}\) (Ans.)
\(\therefore \mathrm{F}=\mathrm{ma}=2500 \times 0.5=1250 \mathrm{~N}(\) Ans. \()\)

\(\mathrm{u}=50 \mathrm{~ms}^{-1}\)
\(\mathrm{~m}=2500 \mathrm{~kg}\)
\(\mathrm{~s}=2500 \mathrm{~m}\)
\(\mathrm{v}=0\)
\(\mathrm{~F}=?, \mathrm{t}=?\)

***প্রশ্নটির ইংরেজি ভার্সনে আদিবেগ \(\mathbf{u}=\mathbf{5 0} \mathrm{ms}^{-1}\) দেওয়া আছে।

প্রশ্ন-02. একজন ক্ষীণ দৃষ্টিসম্পন্ন ব্যক্তির চোখের দূর বিন্দুর দূরত্ব 50 cm।
কি ধরনের এবং কত ক্ষমতার লেন্স ব্যবহার করলে তার চোখের এই ক্রটি দূর হবে?

সমাধান:

\(\mathrm{P}=\frac{1}{\mathrm{u}}+\frac{1}{\mathrm{~V}}\)
\(\Rightarrow P=\frac{1}{\infty}+\frac{1}{(-0.5)}\)
\(\Rightarrow P=-2 \mathrm{D}\) এবং অবতল লেন্স।(Ans.)

\(\mathrm{u}=\infty\) (অসীম)
\(\mathrm{v}=-50 \mathrm{~cm}=-0.5 \mathrm{~m}\)
\(\mathrm{P}=?\)

প্রশ্ন-03. একটি বস্তু সরল দোল গতিতে \(\mathbf{x}=6.0 \cos (6 \pi t+\pi) \mathrm{m}\)
সমীকরণ অনুযায়ী দুলছে। বস্তুর গতির কম্পাঙ্ক কত? t = 2 s সময়ে বস্তুটির বেগ ও ত্বরণের মান কত?

সমাধান:
\(x=6 \cos (6 \pi t+\pi)\) কে
\(\mathrm{x}=\mathrm{A} \cos (\omega \mathrm{t}+\delta)\) এর সাথে তুলনা করে পাই,
\(\omega=6 \pi \Rightarrow 2 \pi \mathrm{f}=6 \pi \Rightarrow \mathrm{f}=3 \mathrm{~Hz}\) (Ans.)
বেগ:
\(\mathrm{v}=\frac{\mathrm{dx}}{\mathrm{dt}}=-6 \sin (6 \pi \mathrm{t}+\pi)(6 \pi+0)\)
t=2s সময়ে বেগ, \(\mathrm{v}=-36 \pi \sin (6 \pi \mathrm{t}+\pi)\)
\(=-36 \pi \sin (12 \pi+\pi)\)
\(=0 \mathrm{~ms}^{-1}\) (Ans.)
ত্বরণ:
\(\mathrm{a}=\frac{\mathrm{d} \mathrm{v}}{\mathrm{dt}}=-36 \pi \cos (6 \pi \mathrm{t}+\pi)(6 \pi+0)\)
\(=-216 \pi^{2} \cos (6 \pi \mathrm{t}+\pi)\)
t=2s সময়ে, \(a=-216 \pi^{2} \cos (12 \pi+\pi)\)
\(=-216 \pi^{2} \mathrm{~ms}^{-2}\) (Ans.)

প্রশ্ন-04. একটি স্থির থোরিয়াম নিউক্লিয়াস (A = 220, Z = 90) হতে
\(\mathbf{E}_{\mathbf{0}}\) গতিশক্তির একটি আলফা কণা নির্গত হয়। বিক্রিয়ায় রেডিয়াম নিউক্লিয়াসের (A = 216, Z = 88) গতিশক্তির কত?

সমাধান:
বিক্রিয়াটি,
\({ }_{90}^{220} \mathrm{Th} \longrightarrow{ }_{88}^{216} \mathrm{Ra}+{ }_{2}^{4} \mathrm{He}+\) গতিশক্তি
\(E=m c^{2}\) সম্পর্ক থেকে পাই,
\(\mathrm{i} . \approx 205424 \mathrm{MeV}\left({ }_{90} \mathrm{Th}^{220}\right)\)
\(\mathrm{ii} . \approx 201000 \mathrm{MeV}\left({ }_{88}^{216} \mathrm{Ra}\right)\)
iii. \(\approx 3757 \mathrm{MeV}\left({ }_{2}^{4} \mathrm{He}\right)\)

সুতরাং, \(205424 \rightarrow 201000+3757+\) গতিশক্তি যেহেতু সমীকরণের দুপাশের শক্তি সংরক্ষণশীল নীতি মেনে চলে, সুতরাং \(\approx 210 \times\) \(10^{3} \mathrm{MeV}\) শক্তি হবে \({ }_{88} \mathrm{R}_{\mathrm{a}}\) নিউক্লিয়াসের জন্য।

রসায়ন

05. \(\mathbf{N}_{2}(\mathrm{~g})+3 \mathrm{H}_{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_{3}(\mathrm{~g}) \quad \Delta \mathrm{H}=-92.38 \mathrm{~kJ}\)
নিম্নে প্রদত্ত প্রশ্নগুলোর উত্তর দাও।
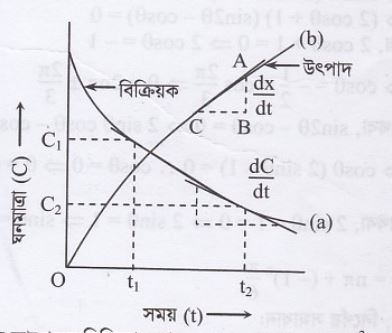
(a) সময়ের সাথে \(\mathbf{N}_{\mathbf{2}}\) ও \(\mathbf{N H}_{3}\) এর পরিমাণের পরিবর্তন চিত্রে দেখাও। উভয়ের সাপেক্ষে সম্মুখ বিক্রিয়ার হার লেখ।

উত্তর : সময়ের সাথে \(\mathbf{N}_{\mathbf{2}}\) ও \(\mathbf{N H}_{3}\) এর পরিমাণের পরিবর্তনের চিত্র :

\(\mathrm{N}_{2}\) এর সাপেক্ষে বিক্রিয়ার হার \(=\mathrm{K} \times\left[\mathrm{N}_{2}\right] \times\left[\mathrm{H}_{2}\right]^{3}\)

\(\mathrm{NH}_{3}\) এর সাপেক্ষে বিক্রিয়ার হার \(=\mathrm{K} \times\left[\mathrm{NH}_{3}\right]^{2}\)

(b) বিক্রিয়াটির সাম্যাবস্থার উপর তাপ ও চাপের প্রভাব কী হবে?

উত্তর :
\(\mathrm{N}_{2}(\mathrm{~g})+3 \mathrm{H}_{2}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_{3}(\mathrm{~g})\) \(\Delta \mathrm{H}=-92.38 \mathrm{KJ}\)

তাপমাত্রার প্রভাব : বিক্রিয়াটি তাপোৎপাদী। লা শ্যাতেলিয়ার নীতি অনুসারে তাপমাত্রা বৃদ্ধিতে সম্মুখ বিক্রিয়ার হার হ্রাস পায়। অর্থাৎ উৎপাদন হ্রাস পায়।
চাপের প্রভাব : বিক্রিয়ায় আয়তনের হ্রাস ঘটে বলে চাপ বৃদ্ধিতে সম্মুখ বিক্রিয়ার হার বৃদ্ধি পায় অর্থাৎ উৎপাদন বাড়ে।

উত্তর : সাম্যাবস্থা ধ্রুবকের (K) উপর প্রভাবকের কোনো প্রভাব নেই ।

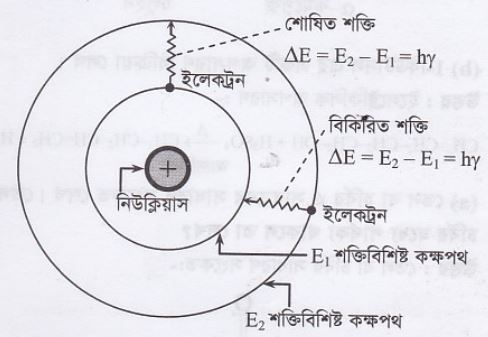
06. (a) বোর মডেল অনুসারে হাইড্রোজন মৌলের বিকিরণ বর্ণালির
উৎপত্তি চিত্রের সাহায্যে দেখাও।

উত্তর : যখন ইলেক্ট্রন নিম্ন শক্তিস্তর হতে উচ্চ শক্তিস্বরে লাফিয়ে চলে তখন আলোক শক্তির শোষণ এবং যখন উচ্চ শক্তিস্তর হতে নিম্ন শক্তিস্তরে লাফিয়ে চলে, তখন আলোক শক্তির বিকিরণ ঘটে। যদি প্রথম কক্ষপথে ইলেক্ট্রনের শক্তি \(\mathrm{E}_{1}\) এবং দ্বিতীয় কক্ষপথে ইলেক্ট্রনের শক্তি \(\mathrm{E}_{2}\) হয়, তবে বিকিরিত আলোর শক্তি হবে \(\Delta \mathrm{E}=\left(\mathrm{E}_{2}-\mathrm{E}_{1}\right)\)। এই শক্তি তড়িৎ চুম্বকীয় বিকিরণ হিসেবে নির্গত হবে ।

চিত্র: বোরের পরমাণু মডেল ও রেখা বর্ণালির উৎস।

(b) হাইড্রোজেন বিকিরণ বর্ণালির পাঁচটি বর্ণালি সারির নাম লেখ।

উত্তর :

লাইম্যান সিরিজ (Lymen Series)
বামার সিরিজ (Balmer Series)
প্যাশ্চেন সিরিজ (Paschen Series)
ব্রাকেট সিরিজ (Brackett Series)
ফুড সিরিজ (Pfund Series)

(c) বোর মডেল এর দুটি সীমাবদ্ধতা লেখ?

উত্তর :

বোর মডেল H পরমাণু ও একক ইলেক্ট্রনবিশিষ্ট আয়নগুলোর (যেমন: \(\mathrm{He}^{+}, \mathrm{Li}^{2+}\)) বর্ণালির ব্যাখ্যা করতে পারলেও একাধিক ইলেক্ট্রনবিশিষ্ট পরমাণুগুলোর বর্ণালির ব্যাখ্যা করতে পারে না।
এক শক্তিস্তর হতে অপর শক্তিস্তরে ইলেক্ট্রনের স্থানাস্তর ঘটলে, বোর পরমাণু মডেল অনুসারে একটি রেখা বর্ণালির সৃষ্টি হওয়ার কথা । কিন্তু উচ্চ ক্ষমতার স্পেকট্রোস্কোপ দ্বারা পরীক্ষায় দেখা যায়, প্রতিটি বর্ণালি রেখা কয়েকটি সূক্ষ্ম রেখা দ্বারা গঠিত। বোর
মডেল এসব সূক্ষ্ম রেখা উৎপত্তির কারণ ব্যাখ্যা করতে পারে না ।

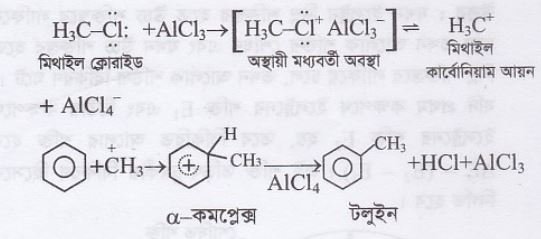
07. (a) বেনজিনের অ্যালকাইলিকরণে ব্যবহৃত বিক্রিয়াটির নাম
কি? বিক্রিয়াটি লেখ ও বিক্রিয়া কৌশল দেখাও।

উত্তর : বেনজিনের অ্যালকাইলিকরণের বিক্রিয়াটির নাম ফ্রিডেল ক্রাফট অ্যালকাইলেশন । এ পদ্ধতিতে বেনজিন বলয়ে অ্যালকাইল মূলক (যেমন: \(\mathrm{CH}_{3}^{+}\)), সরাসরি প্রবেশ করানো হয়। অনার্দ্র \(\mathrm{AlCl}_{3}\) এর উপস্থিতিতে বেনজিন ও মিথাইল ক্লোরাইড বিক্রিয়া করে মিথাইল কেনজিন বা টলুইন উৎপন্ন করে।

বিক্রিয়া কৌশল :

(b) 1-বিউটানল এর একটি অপসারণ বিক্রিয়া লেখ।

উত্তর : ইলেক্ট্রেফিলিক অপসারণ :
\(\mathrm{CH}_{3} \mathrm{CH}_{2}-\mathrm{CH}_{2}-\mathrm{CH}_{2}-\mathrm{OH}+\mathrm{H}_{2} \mathrm{SO}_{4} \stackrel{\Delta}{\longrightarrow} \mathrm{CH}_{3}-\mathrm{CH}_{2}-\mathrm{CH}=\mathrm{CH}_{2}+\mathrm{H}_{2} \mathrm{O}\)
অ্যালকিন

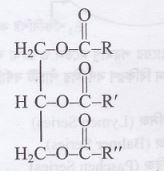
08. (a) তেল বা চর্বির ও সাবানের সাধারণ সংকেত লেখ । তেল ও
চর্বির মধ্যে পার্থক্য থাকলে তা লেখ?

উত্তর : তেল বা চর্বির সাধারণ সংকেত:

সাবানের সাধারণ সংকেত :

\(\mathrm{R}-\mathrm{COO}-\mathrm{Na}^{+}\)
তেল ও চর্বির মধ্যে পাথর্ক: তেল ও চর্বি দুটোই ট্রাইগ্লিসারাইড। কিন্তু তেল ও চর্বি গঠনকারী ফ্যাটি এসিডের অসম্পৃক্ত কার্বনের সংখ্যার পার্থক্য থাকে । তেল কক্ষ তাপমাত্রায় তরল ও চর্বি কক্ষতাপমাত্রায় কঠিন হয়। তেল সাধারণত উদ্ভিদ থেকে আহরিত হয় ও চর্বি সাধারণত প্রাণী থেকে আহরিত হয়।

(b) কেরোসিন ও সয়াবিন তেলের মধ্যে পার্থক্য থাকলে তা লেখ?

উত্তর : অপরিশোধিত পেট্রোলিয়ামের আংশিক পাতনের সাহাযে কেরোসিন পাওয়া যায়। অর্থাৎ এটি পেট্রোলিয়ামের অংশ । এখানে বিভিন্ন হাইড্রোকার্বনের সংমিশ্রণ থাকে। অপরদিকে, সয়াবিন তেল একটি উদ্ভিদ তেল, এখানে মূলত অস্পৃক্ত হাইড্রোকার্বন থাকে।

গণিত

09. যদি \(f(x)=-\sqrt{x-1}\) এর বিপরীত ফাংশন \(\mathbf{f}^{-1}(\mathbf{x})\) হয় তবে
দেখাও যে, \(\mathbf{f}\left(\mathbf{f}^{-1}(\mathbf{x})\right)=\mathbf{f}^{-1}(\mathbf{f}(\mathbf{x}))\)

সমাধান : \(f(x)=-\sqrt{x-1}\)
ধরি, \(f(x)=y \Rightarrow x=f^{-1}(y)\)
\(\therefore y=-\sqrt{x-1} \Rightarrow y^{2}=x-1 \Rightarrow x=y^{2}+1 \Rightarrow f^{-1}(y)=y^{2}+1\)
\(\therefore \mathrm{f}^{-1}(\mathrm{x})=\mathrm{x}^{2}+1\)
\(\therefore \mathrm{f}\left(\mathrm{f}^{-1}(\mathrm{x})\right)=-\sqrt{\mathrm{x}^{2}+1-1}=\mathrm{x} ; \mathrm{x}<0\)
আবার,\(f(x)=-\sqrt{x-1}\)
\(\Rightarrow \mathrm{f}^{-1}(\mathrm{f}(\mathrm{x}))=(-\sqrt{\mathrm{x}-1})^{2}+1=\mathrm{x}-1+1=\mathrm{x}\)
\(\therefore \mathrm{f}\left(\mathrm{f}^{-1}(\mathrm{x})\right)=\mathrm{f}^{-1}(\mathrm{f}(\mathrm{x}))\)
[Showed]

10. \(1+\frac{3}{1 !}+\frac{5}{2 !}+\frac{7}{3 !}+\ldots \ldots\) ধারাটির যোগফল বের কর।

সমাধান : \(1+\frac{3}{1 !}+\frac{5}{2 !}+\frac{7}{3 !}+\ldots .\)
ধরি,
\(U_{r}=\frac{2 r-1}{(r-1) !}=\frac{2 r-2+1}{(r-1) !}\)
\(=\frac{2(r-1)}{(r-1) !}+\frac{1}{(r-1) !}=\frac{2}{(r-2) !}+\frac{1}{(r-1) !}\)
\(\therefore \mathrm{S}_{\mathrm{n}}=\sum \mathrm{U}_{\mathrm{r}}=2 \sum \frac{1}{(\mathrm{r}-2) !}+\sum \frac{1}{(\mathrm{r}-1) !}=2 \mathrm{e}+\mathrm{e}=3 \mathrm{e}\)

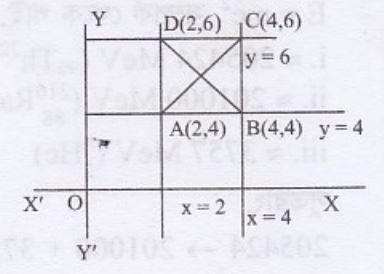
11. x = 2, x = 4, y = 4 এবং y = 6 রেখা দ্বারা গঠিত বর্গক্ষেত্রের
কর্ণদ্বয়ের সমীকরণ বের কর।
সমাধান :

AC কর্ণের সমীকরণ,
\(\frac{x-2}{2-4}=\frac{y-4}{4-6}\)
\(\Rightarrow \frac{x-2}{-2}=\frac{y-4}{-2}\)
\(\Rightarrow x-y+2=0\) (Ans).
BD কর্ণের সমীকরণ,
\(\frac{x-4}{4-2}=\frac{y-4}{4-6} \Rightarrow \frac{x-4}{2}=\frac{y-4}{-2} \Rightarrow x+y-8=0\) (Ans)

12. সমাধান কর: \(\sin \theta+\sin 2 \theta+\sin 3 \theta=1+\cos \theta+\cos 2 \theta\)

সমাধান:
\(\sin \theta+\sin 2 \theta+\sin 3 \theta=1+\cos \theta+\cos 2 \theta\)
\(\Rightarrow \sin 3 \theta+\sin \theta+\sin 2 \theta=1+\cos 2 \theta+\cos \theta\)
\(\Rightarrow 2 \sin \frac{3 \theta+\theta}{2} \cos \frac{3 \theta-\theta}{2}+\sin 2 \theta=2 \cos ^{2} \theta+\cos \theta\)
\(\Rightarrow 2 \sin 2 \theta \cos \theta+\sin 2 \theta=2 \cos ^{2} \theta+\cos \theta\)
\(\Rightarrow \sin 2 \theta(2 \cos \theta+1)=\cos \theta(2 \cos \theta+1)\)
\(\Rightarrow \sin 2 \theta(2 \cos \theta+1)-\cos \theta(2 \cos \theta+1)=0\)
\(\Rightarrow(2 \cos \theta+1)(\sin 2 \theta-\cos \theta)=0\)
হয়, \(2 \cos \theta+1=0 \Rightarrow 2 \cos \theta=-1\)
\(\Rightarrow \cos \theta=-\frac{1}{2}=\cos \frac{2 \pi}{3} \Rightarrow \theta=2 n \pi \pm \frac{2 \pi}{3}\)
অথবা, \(\sin 2 \theta-\cos \theta=0 \Rightarrow 2 \sin \theta \cos \theta-\cos \theta=0\)
\(\Rightarrow \cos \theta(2 \sin \theta-1)=0 \therefore \cos \theta=0 \Rightarrow \theta=(2 \mathrm{n}+1) \frac{\pi}{2}\)
অথবা, \(2 \sin \theta-1=0 \Rightarrow 2 \sin \theta=1 \Rightarrow \sin \theta=\frac{1}{2}=\sin \frac{\pi}{6}\)
\(\theta=\mathrm{n} \pi+(-1)^{\mathrm{n}} \frac{\pi}{6}\)
\(\theta=n \pi+(-1)^{\mathrm{n}} \frac{\pi}{6}\)
\(\therefore\) নির্ণেয় সমাধান: \(\theta=2 n \pi \pm \frac{2 \pi}{3},(2 n+1) \frac{\pi}{2}, n \pi+(-1)^{n} \frac{\pi}{6}\) যখন \(n \in z\)

13. সালোকসংশ্লেষণের রাসায়নিক বিক্রিয়াটি লিখ এবং
সালোকসংশ্লেষণের দুইটি গুরুত্বপূর্ণ কাজ উল্লেখ কর।

উত্তর: সালোকসংশ্লেষণের রাসায়নিক বিক্রিয়া:

সালোকসংশ্লেষণের দুটি গুরুত্বপূর্ণ কাজ নিচে উল্লেখ করা হল

শক্তির উৎস: জীবজগতের শক্তির একমাত্র উৎস হল।
সালোকসংশ্লেষণ প্রক্রিয়া। খাদ্যের মধ্যে এ শক্তি আসে সূর্য
হতে। সূর্যের এ শক্তি সালোকসংশ্লেষণ প্রক্রিয়ায় খাদ্যে রাসায়নিক শক্তি হিসেবে সঞ্চিত থাকে। কাজেই জীবের সকল শক্তির উৎস এ প্রক্রিয়া।
পরিবেশ পরিশোধন: সালোকসংশ্লেষণ প্রক্রিয়ায় CO,
শোষিত হয় এবং 0, উৎপন্ন হয়। প্রাণিকুলের জন্য ক্ষতিকারক CO, শোষণ করে এবং সকল জীবের শ্বসনের জন্য N, সরবরাহ করে এ প্রক্রিয়া পরিবেশ পরিশোধন করে থাকে। এভাবে সবুজ উদ্ভিদের এ প্রক্রিয়া জীবজগতকে
নিশ্চিত ধ্বংসের হাত থেকে রক্ষা করে।

14. একবীজপত্রী উদ্ভিদের মূলের অন্তর্গঠনগত শনাক্তকারী ছয়টি
বৈশিষ্ট্য লিখ।

উত্তর: একবীজপত্রী উদ্ভিদের মূলের অন্তর্গঠনগত শনাক্তকারী বৈশিষ্ট্যসমূহ:

ত্বকে কিউটিকল অনুপস্থিত। এতে এককোষী রোম আছে।
অধঃত্বক অনুপস্থিত।
পরিচক্র একসারি কোষ দিয়ে গঠিত।
ভাস্কুলার বান্ডল অরীয় এবং একান্তরভাবে সজ্জিত।
মেটাজাইলেম কেন্দ্রের দিকে এবং প্রোটোজাইলেম পরিধির
দিকে অবস্থিত।
জাইলেম বা ফ্লোয়েম গুচ্ছের সংখ্যা ছয় এর অধিক |

15. গণ পর্যন্ত মানুষের শ্রেণিবিন্যাস কর (পর্ব, উপ-পর্ব, শ্রেণি, বর্গ, গোত্রসহ)।

উত্তর: মানুষের শ্রেণিবিন্যাস:
পর্ব – Chordata
উপপর্ব – Vertebrata
  শ্রেণি – Mammalia
   বর্গ – Primates
    উপবর্গ – Hominoidea
     গোত্র – Hominidae
      গণ – Homo

16. নিম্নোক্ত প্রাণীদের বৈজ্ঞানিক নাম লিখ।

a. গোলকৃমি b. আপেল শামুক c. জোঁক

d. রুইমাছ e. ঘড়িয়াল f. দোয়েল

উত্তর: প্রাণীদের বৈজ্ঞানিক নাম নিচে উল্লেখ করা হলো:

প্রাণীর নাম	বৈজ্ঞানিক নাম
(a) গোলকৃমি	Ascaris lambricoides
(b) আপেল শামুক	Pila globosa
(c) জোঁক	Hiradinaria manillensis
(d) রুইমাছ	Labeo rohita
(e) ঘড়িয়াল	Gavialis gangeticus
(f) দোয়েল	Copsychus saularis

বাংলা

17. সারমর্ম লেখ (অনধিক চার বাক্যে) :
আসিতেছে শুভদিন,
দিনে দিনে বহু বাড়িয়াছে দেনা, শুধিতে হইবে ঋণ!
হাতুড়ি শাবল গাঁইতি চালায়ে ভাঙিল যারা পাহাড়,
পাহাড়-কাটা সে পথের দুপাশে পড়িয়া যাদের হাড়,
তোমারে সেবিতে হইল যাহারা মজুর, মুটে ও কুলি,
তোমারে বহিতে যারা পবিত্র অঙ্গে লাগাল ধূলি;
তারাই মানুষ, তারাই দেবতা, গাহি তাহাদেরি গান,
তাদের ব্যথিত বক্ষে পা ফেলে আসে নব উত্থান!

সারমর্ম: শ্রমজীবী মানুষের শ্রমে-ঘামে ও রক্তে জীবনের বিনিময়ে গড়ে উঠেছে স্বাচ্ছন্দ্যময় সভ্যতা। তাদের নিরলস পরিশ্রমে আমরা সুখে দিনযাপন করতে সক্ষম হয়েছি। কিন্তু সমাজে এ দেবতাতুল্য মানুষ নানাভাবে শোষিত, বঞ্চিত ও উপেক্ষিত। এরাই একদিন
নবজাগরণের মধ্যদিয়ে বিশ্বে পালাবদলের সূচনা করবে।

18. ভাব সম্প্রসারণ কর (অনধিক ছয় বাক্যে) :
গ্রন্থগত বিদ্যা আর পরহস্তে ধন।
নহে বিদ্যা, নহে ধন, হলে প্রয়োজন।

মূলভাব: অর্জিত সম্পদ ও অর্জিত জ্ঞান যথাসময়ে কাজে লাগানো। গেলেই শুধু সার্থকতা প্রমাণিত হতে পারে। কিন্তু যে জ্ঞান ও অর্থসম্পদ মানুষের প্রয়োজনের সময় কাজে লাগানো যায় না, তার কোনো মূল্য নেই।
ভাব সম্প্রসারণ: গ্রন্থগত বিদ্যা যা আত্মস্থ করা হয়নি এবং এমন ধন-সম্পদ যা নিজের করায়ত্ত হয়নি- এ সমস্তই নিরর্থক। কারণ। প্রয়োজনীয় মুহূর্তে এগুলোর যথাযথ ব্যবহার করা সম্ভব হয় না। পৃথিবীতে মানুষের জীবনে ধন-সম্পদ ও বিদ্যার গুরুত্ব। অপরিসীম। কিন্তু বিদ্যা যদি গ্রন্থের ভেতরেই মলাটবদ্ধ অবস্থায়। অব্যবহৃত হয়ে পড়ে থাকে, মানুষ যদি তা আত্মস্থ না করে কিংবা আত্মস্থ করে চলমান জীবনে কাজে লাগাতে না পারে, তবে সে বিদ্যা মূলত কোনো বিদ্যাই নয় । মলাটবদ্ধ গ্রন্থের বিদ্যাকে মানুষের জীবনে প্রয়োগ করতে হবে। তবেই সে বিদ্যা পৃথিবীর মানুষের কল্যাণ বয়ে আনবে। অন্যদিকে, নিজের অর্জিত ধনসম্পত্তি যদি অন্যের কাছে রক্ষিত থাকে, তবে প্রয়োজনের সময় সেই সম্পত্তি উদ্ধার করাও অনেক সময় সমস্যা হয়ে দাঁড়ায় । বরং নিজের কাছে থাকা সম্পত্তিই প্রয়োজনের সময় ব্যবহার করা সম্ভব। সুতরাং সার্থক ও সুন্দর জীবনের প্রয়োজনে বিদ্যাকে গ্রন্থের বন্দিশালা হতে মুক্ত করে আত্মস্থ করতে হবে, পরের হাতে রক্ষিত সম্পত্তি নিজের করায়ত্ত করতে হবে। বিদ্যা ও সম্পদ তখনই সার্থক হয়ে ওঠে যখন মানুষের যথার্থ প্রয়োজন মিটায় । কিন্তু মানুষের যথার্থ প্রয়োজনে যদি তা কাজে না লাগানো যায়, তবে সেই বিদ্যা ও অর্থ বিফলতার নামান্তর।
মন্তব্য: পরিশেষে বলা যায় জ্ঞান ও বিদ্যা জীবনের কাজে লাগাতে হবে, আর তাতেই প্রতিপন্ন হবে মানবজীবনের সার্থকতা। কেননা, প্রয়োজনের সময় সম্পদ ও বিদ্যা নিজের হস্তগত থাকা অপরিহার্য।

19. বাংলাদেশের মুক্তিযুদ্ধ’ নিয়ে ৬টি বাক্য লেখ।

উত্তর : বাঙালির জাতীয় জীবনে সবচেয়ে গৌরবোজ্জ্বল ঘটনা বাংলাদেশের মুক্তিযুদ্ধ। ১৯৭১ সালে মুক্তিযুদ্ধের মধ্য দিয়েই বাঙালি স্বাধীন জাতি হিসেবে সারা বিশ্বে পরিচিতি লাভ করে। বাঙালি জাতি ১৯৭১ সালে বঙ্গবন্ধুর ৭ মার্চের ভাষণে অনুপ্রাণিত হয়ে স্বতঃস্ফূর্তভাবে মুক্তিযুদ্ধে যোগদান করেছিল। ১৯৭১ সালের ১০ এপ্রিল গঠিত মুজিবনগর সরকার বাংলাদেশের রণাঙ্গনকে ১১টি সেক্টরে ভাগ করে প্রত্যেকটির জন্য একজন করে সেক্টর কমান্ডারও নিযুক্ত করেন। এভাবেই অস্থায়ী সরকারের তত্ত্বাবধানে দীর্ঘ নয় মাসের সশস্ত্র মুক্তিযুদ্ধের পর বাংলাদেশ অবশেষে স্বাধীনতার লাল সূর্য ছিনিয়ে আনতে সক্ষম হয়। মুক্তিযুদ্ধের সময় দেশমাতৃকার টানে বাংলাদেশের মানুষ আত্মত্যাগের যে দৃষ্টান্ত রেখেছে তা ইতিহাসে বিরল তাইতো কবি সুকান্ত ভট্টাচার্যের কণ্ঠে ধ্বনিত হয়েছে-
সাবাস বাংলাদেশ, এ পৃথিবী।
অবাৰু তাকিয়ে রয়;
জ্বলে-পুড়ে-মরে ছারখার
তবু মাথা নোয়াবার নয়।

20. বিপরীত শব্দ লেখ :
আসমান
স্থূলবুদ্ধি
কাল্পনিক

উত্তর

শ্ব্দ	বিপরীত শব্দ
আসমান	জমিন
স্কুলবুদ্ধি	সূক্ষ্মবুদ্ধি
কাল্পনিক	বাস্তবিক

English

21. Hold fast to dreams
For if dreams die
Life is a broken-winged bird
That cannot fly
Which poem are these lines taken from? Who is the writer of the poem? What does he mean by “Life is a broken-winged bird”?

Ans: These lines are taken from the poem Dreams written by American poet James Mercer Langston Hughes (1902-1967). The poem is quite short, comprising of two stanzas only including eight lines long. Langston Hughes starts out his poem, Dreams by immediately concerning readers with a piece of advice: ‘Hold fast to dreams’ In the very first line, he mentions the readers about the importance of dreams in our life. The dreams of future progress our life and help to achieve the goals. If our dreams die, our life can be brutal, meaningless and hopeless. The poet uses the phrase ‘a broken-winged bird’ at three line in the first stanza as a metaphor. In literature, the bird symbolizes hope, ecstasy and liberty. “Brokenwinged bird’ means hopeless, joylessness and slavery. The poet means by the line ‘Life is a brokenwinged bird’ that a person becomes purposeless and hopeless without dreams.

22. Write six sentences on ‘The influcence of culture
on adolescents’

Ans: The influence of culture for on adolescence Adolescence is a stage of development, a period of transition between childhood and adulthood. All adolescents go through changes; physical changes, social and emotional changes and the process of developing their individual identity. They came from different backgrounds are influenced by different cultural norms and different attitudes towards values and norms in society. Parents and family life are the foundations for building an adolescence’s personality and identity, instilling values and social norms. Parenting practices are influenced by culture and an adolescent’s upbringing is affected by ethnic group, values and traditions that he belongs to. So culture has a strong influence on development, behavior, values and beliefs. Family rituals and good communication have a positive affect on adolescents. Parents who instill positive cultural values and beliefs in their children help raise their self-cteem and
academic success.

23. Write six sentences on the importance of
biodiversity for our livelihood.

Ans: The importance of biodiversity for our livelihood Biodiversity is the existence of a large number of different kinds of animals and plants which make a balanced environment. Millions people depend on nature and species for their day-to-day livelihood. Biodiversity has an important role for our livelihood. Because biodiversity provides many sources of food, fuel, medicines and other products of natural materials. People can use these for earning source. Nature-related tourism is also a significant income generator for many people.

24. What is rhyme? why do writers use rhyme in poems?

Ans: Rhyme: Rhyme is a repetition of similar sounding words, occuring at the end of lines in poem or songs. A rhyme is a tool utilizing repeating patterns that bring rhythm or musicality to poems.
“Shall I compare thee to a summer’s day?
Thou art more lovely and more temperate:
Rough winds do shake the darling buds of May, And summer’s lease hath all too short a date:’ (Sonnet 18 by William Shakespeare) There are different types of rhymes used in poems.

End Rhyme
Internal Rhyme
Slant Rhyme
Rich Rhyme
Eye Rhyme
Identical Rhyme

The writers make a poem musical to readers by using the rhyme. The writers use it to make a poem musical and